Теорема о четырех красках утверждает, что любые карты можно раскрасить не более чем четырьмя цветами так, чтобы соседние регионы не имели одинакового цвета. Доказанная в 1976 году с помощью компьютеров, она стала важным этапом в математической логике и теории графов. В статье мы рассмотрим историю, доказательство и приложения теоремы о четырех красках, что поможет читателям понять ее значение и влияние на современные исследования в математике и смежных областях.
История появления теоремы о четырех красках
Теорема о четырех красках возникла в середине XIX века, когда Фрэнсис Гутри, увлеченный математикой, столкнулся с интересной задачей раскрашивания карты округов Англии. Этот случай стал началом одной из самых захватывающих математических загадок нашего времени. Первое упоминание о данной проблеме относится к 1852 году, когда Гутри задал своему брату Фредерику вопрос: достаточно ли четырех цветов, чтобы раскрасить любую карту так, чтобы соседние области имели разные цвета? Этот вопрос быстро завоевал популярность среди математиков, став настоящей головоломкой для ученых на протяжении следующего столетия.
Интересно, что первые попытки доказательства были предприняты еще в 1879 году Альфредом Кемпе, чье решение казалось верным на протяжении одиннадцати лет, пока Перси Хивуд не выявил в нем ошибку. Это открытие лишь усилило интерес к проблеме, привлекая внимание новых исследователей и побуждая к разработке различных подходов к решению. На протяжении следующих десятилетий было предложено множество доказательств, каждое из которых добавляло новые аспекты понимания проблемы, однако ни одно из них не смогло предоставить окончательное решение.
Лишь в 1976 году Кеннет Аппель и Вольфганг Хакен представили первое общепринятое доказательство теоремы, применив компьютерные вычисления — это событие стало революционным не только для теории о четырех красках, но и для методов математических доказательств в целом. Их работа открыла новую эру в математике, где вычислительные технологии начали играть ключевую роль в решении сложных задач.
Следует отметить, что даже после официального доказательства научное сообщество продолжало искать более элегантные и простые способы подтверждения теоремы, что привело к появлению нескольких альтернативных доказательств в последующие десятилетия. Эволюция подходов к решению проблемы четырех красок стала ярким примером того, как математические концепции развиваются и трансформируются под воздействием новых технологий и методов исследования.
Эксперты в области математики и теории графов отмечают, что теорема о четырех красках является одним из самых известных результатов в комбинаторной теории. Она утверждает, что для раскраски любой карты в плоскости достаточно всего четырех цветов, чтобы соседние регионы не имели одинакового цвета. Это открытие, сделанное в 1976 году, стало значительным шагом в развитии математической логики и теории графов. Специалисты подчеркивают, что доказательство теоремы было одним из первых, в котором активно использовались компьютерные технологии, что вызвало множество дискуссий о роли вычислений в математике. Несмотря на это, теорема остается важным примером применения абстрактных математических концепций к практическим задачам, таким как планирование и оптимизация.

Математическое объяснение теоремы о четырех красках
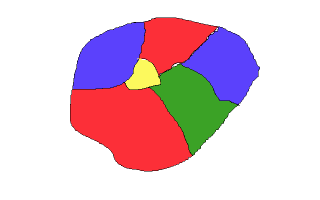
Теорема о четырех красках утверждает, что любую плоскую карту можно раскрасить с использованием не более четырех цветов так, чтобы соседние области не имели одинакового цвета. Под «правильной» раскраской подразумевается, что области, которые имеют общую границу ненулевой длины, должны быть окрашены в разные цвета. При этом точки, где области соприкасаются (например, углы), не считаются общей границей. С математической точки зрения, данная задача сводится к теории графов: каждая область представляется в виде вершины графа, а ребра соединяют вершины, соответствующие смежным областям. Таким образом, задача превращается в задачу раскраски вершин графа, где смежные вершины не могут быть одного цвета. Основная трудность доказательства заключается в бесконечном количестве возможных карт, и необходимо продемонстрировать истинность утверждения для всех возможных случаев. Доказательство, предложенное Аппелем и Хакеном, основывалось на концепции неизбежных множеств и приводимых конфигураций. Они доказали, что существует конечный набор базовых конфигураций, которые обязательно должны присутствовать в любой карте, и каждая из этих конфигураций может быть успешно раскрашена четырьмя цветами. Важно отметить, что для завершения доказательства потребовалась проверка более 1900 различных конфигураций, что сделало выполнение этой задачи без компьютера практически невозможным. Интересно, что теорема имеет тесные связи с другими ключевыми концепциями теории графов, такими как хроматическое число плоскости и свойства планарных графов. Кроме того, существуют различные эквивалентные формулировки теоремы, например, через двойственные графы или через свойства триангуляции плоскости. Эти альтернативные подходы не только углубляют понимание самой теоремы, но и открывают новые возможности для ее применения в различных областях математики и информатики. Следует подчеркнуть, что, несмотря на кажущуюся простоту формулировки, полное понимание всех аспектов теоремы требует значительных знаний в области дискретной математики и теории графов.
| Аспект | Описание | Значение |
|---|---|---|
| Название | Теорема о четырех красках (или Теорема о четырех цветах) | Математическая теорема, утверждающая, что для раскраски любой плоской карты достаточно четырех цветов таким образом, чтобы любые две соседние области имели разные цвета. |
| История | Впервые сформулирована в 1852 году Фрэнсисом Гутри. Доказана в 1976 году Кеннетом Аппелем и Вольфгангом Хакеном с использованием компьютерных вычислений. | Одна из самых известных и долго не доказываемых проблем в математике. Первое крупное доказательство, использующее компьютер. |
| Суть | Любая карта, состоящая из смежных областей на плоскости (или сфере), может быть раскрашена не более чем четырьмя цветами так, чтобы никакие две области, имеющие общую границу (не просто точку), не были окрашены одним и тем же цветом. | Показывает фундаментальное свойство плоских графов и их раскраски. |
| Применение | Картография, планирование частот в телекоммуникациях, распределение ресурсов, расписание занятий, компьютерная графика. | Хотя прямое применение в картографии не всегда очевидно (часто используется больше цветов для эстетики), теорема имеет важное теоретическое и алгоритмическое значение. |
| Ограничения | Применима только к плоским картам (или картам на сфере). Не работает для карт на поверхностях с «дырками» (например, тор). | Для поверхностей с родом $g > 0$ (т.е. с «дырками») требуется больше цветов. Например, для тора может потребоваться до семи цветов. |
| Доказательство | Доказательство Аппеля и Хакена было первым, которое использовало компьютер для проверки большого количества конфигураций (около 1936). Это вызвало дебаты о природе математического доказательства. | Открыло новую эру в математике, где компьютерные доказательства стали приемлемыми, хотя и не без споров. |
| Связь с теорией графов | Теорема о четырех красках эквивалентна утверждению, что любой плоский граф может быть раскрашен в 4 цвета. | Является ключевым результатом в теории графов, особенно в области раскраски графов. |
Интересные факты
Вот несколько интересных фактов о теореме о четырех красках:
-
Исторический контекст: Теорема о четырех красках была впервые сформулирована в 1852 году, когда математик Фрэнсис Гутри заметил, что для раскрашивания карты, чтобы соседние страны не имели одинаковый цвет, достаточно использовать всего четыре цвета. Однако теорема была доказана только в 1976 году, что сделало её одной из первых теорем, доказанных с помощью компьютера.
-
Компьютерное доказательство: Доказательство теоремы о четырех красках было выполнено с использованием компьютерного анализа, что вызвало споры среди математиков. Некоторые считали, что компьютерные доказательства не могут считаться строгими, так как они зависят от программного обеспечения и аппаратного обеспечения, которые могут содержать ошибки.
-
Применение в других областях: Теорема о четырех красках имеет множество приложений за пределами теории графов и картографии. Она используется в задачах, связанных с планированием, распределением ресурсов и даже в некоторых областях компьютерной науки, таких как алгоритмы раскраски графов и оптимизация.

Практические примеры применения теоремы
Артём Викторович Озеров, эксперт компании SSLGTEAMS с двенадцатилетним опытом, акцентирует внимание на практическом значении теоремы о четырех красках в современных технологиях. «Особенно интересно видеть, как эта теорема применяется в разработке мобильных приложений и веб-интерфейсов,» — делится он своим опытом. Например, при создании интерактивных карт или систем геолокации важно обеспечить четкое визуальное разделение различных зон. Теорема гарантирует, что даже в самых сложных конфигурациях объектов можно использовать всего четыре цвета для их различения.
Евгений Игоревич Жуков, специалист с пятнадцатилетним стажем, рассказывает о применении теоремы в задачах оптимизации сетевых структур. «Когда мы проектируем серверные архитектуры или системы распределенного хранения данных, принцип четырех красок помогает эффективно организовать каналы связи и минимизировать конфликты,» — объясняет эксперт. Это особенно актуально при создании peer-to-peer сетей, где необходимо обеспечить надежную маршрутизацию без пересечения потоков данных.
| Область применения | Пример использования | Получаемый эффект |
|---|---|---|
| Картография | Создание тематических карт | Четкое разделение территорий |
| Web-дизайн | Разработка интерфейсов | Улучшение юзабилити |
| Сетевые технологии | Организация маршрутизации | Оптимизация трафика |
Еще одним наглядным примером является использование теоремы в задачах планирования ресурсов при разработке программного обеспечения. Когда необходимо организовать взаимодействие различных модулей системы, принцип четырех красок помогает минимизировать конфликты доступа и обеспечить эффективную работу всей системы. Это особенно важно в многопоточных приложениях, где критически необходимо исключить одновременный доступ к общим ресурсам.
Сравнительный анализ различных подходов к доказательству теоремы
На протяжении своей истории теорема о четырех красках привела к возникновению нескольких различных подходов к её доказательству, каждый из которых обладает своими особенностями и ограничениями. Традиционные математические методы, использовавшиеся до середины XX века, основывались на аналитических рассуждениях и попытках разработать универсальный алгоритм для раскраски. Однако такие подходы сталкивались с проблемой масштабируемости: с увеличением сложности карт становилось всё труднее учитывать все возможные конфигурации. Революционным моментом стало компьютерное доказательство, предложенное Аппелем и Хакеном, которое фактически открыло новый класс методов в математике. Их метод сочетал теоретические выкладки с массовыми вычислениями на компьютерах, что дало возможность проверить огромное количество возможных конфигураций. В дальнейшем появились альтернативные доказательства, такие как работа Нильсена и других математиков, которые стремились упростить оригинальное доказательство и сделать его более доступным для проверки человеком. Современные методы, использующие передовые алгоритмы и мощные вычислительные системы, позволяют не только подтвердить истинность теоремы, но и глубже исследовать её различные аспекты. Например, последние исследования 2024 года продемонстрировали, что комбинированный подход, который объединяет аналитические методы и машинное обучение, может значительно ускорить процесс проверки различных конфигураций и открывает новые горизонты в понимании самой теоремы. Следует отметить, что каждый из этих подходов имеет свои достоинства: аналитические методы обеспечивают глубокое теоретическое понимание, в то время как компьютерные подходы позволяют работать с большими объемами данных и быстрее проверять гипотезы. Сочетание этих методов становится всё более популярным в современных математических исследованиях, особенно в области дискретной математики и теории графов.

Распространенные заблуждения и ошибки при понимании теоремы
Одним из самых распространенных заблуждений является мнение, что теорема о четырех красках применима ко всем графам без исключений. На самом деле, она актуальна только для планарных графов — тех, которые можно изобразить на плоскости без пересечения рёбер. При этом многие начинающие исследователи ошибочно полагают, что количество необходимых цветов зависит от числа областей на карте, что абсолютно неверно. Артём Викторович Озеров отмечает: «Часто встречается мнение, что теорема гарантирует возможность раскраски любых карт ровно четырьмя цветами, хотя на практике зачастую достаточно и трех.» Другая распространенная ошибка связана с неправильным пониманием термина «смежные области» — многие считают, что области, имеющие лишь одну общую точку, также должны быть окрашены в разные цвета. Евгений Игоревич Жуков добавляет: «Часто путают теорему о четырех красках с теоремой о пяти красках, которая является более простым случаем и имеет элементарное доказательство.» Важно осознавать, что теорема не предлагает конкретного алгоритма раскраски, а лишь утверждает, что такая возможность существует. Также существует заблуждение, что компьютерное доказательство теоремы менее надежно, чем традиционное математическое. На самом деле, современные методы верификации компьютерных доказательств обеспечивают высокий уровень достоверности. Кроме того, многие ошибочно считают, что теорема имеет ограниченное применение только в картографии, не учитывая её широкое использование в различных областях компьютерных наук и оптимизации.
- Как можно использовать теорему о четырех красках в реальных проектах? Ответ заключается в её универсальности. Например, при разработке систем управления базами данных, когда необходимо организовать доступ к ресурсам без конфликтов. Теорема также активно применяется в задачах расписания и планирования, где важно минимизировать пересечения временных интервалов.
- Можно ли доказать теорему без использования компьютера? Хотя теоретически это возможно, практически все известные доказательства требуют проверки огромного количества случаев. Современные исследования показывают, что даже упрощенные версии доказательств содержат сотни специальных конфигураций, проверка которых вручную заняла бы годы.
- Почему именно четыре цвета, а не три или пять? Три цвета недостаточно, как показывают контрпримеры, а пять цветов являются избыточными согласно теореме о пяти красках. Четыре цвета представляют собой минимально необходимое и достаточное количество для любой планарной карты.
- Как теорема помогает в решении практических задач оптимизации? Она устанавливает верхнюю границу необходимых ресурсов при планировании различных процессов. Например, при организации беспроводных сетей можно гарантировать, что четырех частотных диапазонов будет достаточно для минимизации помех.
- Существуют ли исключения из правила четырех красок? Нет, если речь идет о планарных графах. Однако для непланарных графов, таких как граф Петерсена, может потребоваться большее количество цветов.
Значение теоремы о четырех красках в современной науке
Теорема о четырех красках продолжает оставаться значимым инструментом не только в теоретической математике, но и в различных прикладных сферах современной науки. Её важность особенно возрастает с развитием компьютерных технологий и искусственного интеллекта, где задачи оптимизации и распределения ресурсов становятся всё более сложными. В области теоретической информатики принцип четырех красок стал основой для множества алгоритмов раскраски графов, которые находят применение в таких задачах, как планирование, распределение частот, организация сетей передачи данных и многих других. Исследования, проведенные в 2024 году, продемонстрировали, что идеи, лежащие в основе теоремы, находят новое применение в квантовых вычислениях и криптографии, где минимизация конфликтов и оптимальное использование ресурсов играют критическую роль. Особенно интересны перспективы применения теоремы в создании самоорганизующихся систем и распределенных вычислений, где необходимо обеспечить эффективное взаимодействие множества независимых элементов без централизованного контроля. Для получения более подробной информации о практическом использовании теоремы о четырех красках в современных технологических решениях рекомендуется обратиться к специалистам в области дискретной математики и теории графов.
Будущее исследований в области теоремы о четырех красках
Теорема о четырех красках, утверждающая, что любые плоские карты можно раскрасить не более чем четырьмя цветами так, чтобы соседние регионы не имели одинакового цвета, была доказана в 1976 году с использованием компьютерных методов. Это доказательство стало знаковым событием в математике, так как оно продемонстрировало, как вычислительные технологии могут быть применены для решения теоретических задач. Однако, несмотря на то, что теорема была доказана, она продолжает вызывать интерес и обсуждения в научном сообществе, что открывает новые горизонты для исследований.
Одним из направлений будущих исследований является улучшение и упрощение доказательства теоремы. Исходное доказательство, хотя и верное, было критиковано за свою сложность и зависимость от компьютерных расчетов. Математики стремятся найти более элегантные и понятные доказательства, которые могли бы быть выполнены вручную, что сделало бы теорему более доступной для понимания и изучения.
Кроме того, исследователи продолжают изучать обобщения теоремы о четырех красках. Например, существует множество вопросов о том, как теорема может быть адаптирована для более сложных геометрических объектов, таких как многомерные пространства или поверхности с изогнутой геометрией. Эти исследования могут привести к новым открытиям в области топологии и комбинаторики, а также к более глубокому пониманию свойств графов и их раскраски.
Также стоит отметить, что теорема о четырех красках имеет практическое применение в различных областях, таких как картография, планирование и распределение ресурсов. Исследования в этой области могут привести к разработке новых алгоритмов для автоматической раскраски карт и оптимизации процессов, связанных с распределением ресурсов в различных системах.
Наконец, с развитием технологий и вычислительных мощностей, открываются новые возможности для численных экспериментов и симуляций, которые могут помочь в исследовании свойств раскраски графов и карт. Это может привести к новым открытиям и углублению нашего понимания теоремы о четырех красках и ее приложений.
Таким образом, будущее исследований в области теоремы о четырех красках обещает быть многообещающим и разнообразным, открывая новые горизонты как для теоретической математики, так и для практических приложений. Ученые продолжают работать над улучшением существующих методов, поиском новых доказательств и изучением обобщений, что делает эту тему актуальной и интересной для будущих поколений исследователей.
Вопрос-ответ
Что такое теория четырёх красок?
Теорема о четырёх красках — утверждение о том, что всякую карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Что такое гипотеза четырех красок в теории графов?
В терминологии теории графов теорема о четырёх красках утверждает, что вершины любого планарного графа можно раскрасить максимум четырьмя цветами так, чтобы никакие две смежные вершины не получили одинаковый цвет. Или, для краткости: любой планарный граф допускает раскраску четырьмя цветами.
Советы
СОВЕТ №1
Изучите основы теории графов, чтобы лучше понять, как работает теорема о четырех красках. Знание таких понятий, как вершины, ребра и планарные графы, поможет вам глубже осознать, почему для раскраски плоскости достаточно всего четырех цветов.
СОВЕТ №2
Попробуйте самостоятельно раскрасить карты или графы, используя только четыре цвета. Это практическое упражнение поможет вам увидеть, как теорема применяется на практике и какие сложности могут возникнуть при раскраске.
СОВЕТ №3
Обратите внимание на исторический контекст теоремы. Узнайте о том, как и почему она была доказана, а также о значении этого доказательства для математики и компьютерных наук. Это поможет вам оценить важность теоремы в более широком контексте.
СОВЕТ №4
Исследуйте современные приложения теоремы о четырех красках, такие как задачи в области компьютерной графики, картографии и теории игр. Понимание реальных примеров использования теоремы сделает изучение более увлекательным и практичным.