Модель регрессии — это инструмент статистического анализа, который выявляет зависимости между переменными и прогнозирует значения одной переменной на основе других. В статье рассмотрим применение регрессии в различных сферах, от экономики до медицины, и её роль в решении задач прогнозирования. Понимание основ регрессии расширит ваши знания в анализе данных и поможет принимать обоснованные решения на основе результатов.
Основные концепции и принципы работы моделей регрессии
Модель регрессии является математическим инструментом, который помогает установить связь между зависимой переменной и одной или несколькими независимыми переменными. Она работает на основе поиска оптимальной функции, которая наиболее точно отражает наблюдаемые данные и может быть использована для предсказания новых значений. Основная задача регрессионного анализа заключается в минимизации разницы между фактическими и предсказанными значениями, что достигается с помощью различных методов оптимизации.
Ключевым компонентом любой регрессионной модели выступает функция потерь, которая измеряет качество подгонки модели к данным. Наиболее часто используемой функцией потерь является среднеквадратическая ошибка (MSE), но также существуют и другие варианты, такие как средняя абсолютная ошибка (MAE) и хьюберовская потеря, каждая из которых имеет свои преимущества в зависимости от типа данных и поставленной задачи. Процесс обучения модели регрессии можно рассматривать как поиск таких параметров, при которых значение функции потерь будет минимальным.
Для лучшего понимания принципа работы можно провести простую аналогию: представьте, что вы пытаетесь подобрать идеальную резинку, которая максимально близко проходит ко всем точкам на графике. Чем точнее вы подберете форму и положение этой резинки, тем лучше ваша модель будет предсказывать новые значения. Важным аспектом является выбор правильной степени сложности модели: слишком простая модель может не в полной мере описать данные (проблема недообучения), в то время как чрезмерно сложная может переобучиться и утратить способность к обобщению.
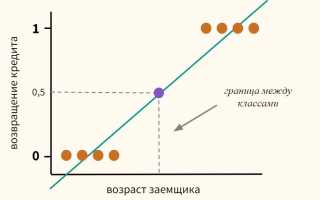
Существует несколько основных типов моделей регрессии, каждая из которых имеет свои особенности применения. Линейная регрессия основывается на предположении о линейной зависимости между переменными, в то время как нелинейные модели могут учитывать более сложные взаимосвязи. Полиномиальная регрессия позволяет моделировать криволинейные зависимости, а логистическая регрессия используется для задач классификации. Все эти варианты объединяет общая цель – найти наиболее подходящее математическое описание исследуемого явления.
Модель регрессии представляет собой мощный инструмент статистического анализа, который позволяет исследовать и предсказывать взаимосвязи между переменными. Эксперты отмечают, что основная цель регрессионного анализа заключается в том, чтобы определить, как изменение одной или нескольких независимых переменных влияет на зависимую переменную. Это может быть особенно полезно в различных областях, таких как экономика, медицина и социология.
Специалисты подчеркивают, что существует несколько типов регрессионных моделей, включая линейную, полиномиальную и логистическую регрессию, каждая из которых имеет свои особенности и применяется в зависимости от характера данных. Кроме того, важным аспектом является проверка качества модели, что позволяет оценить, насколько точно она описывает наблюдаемые данные. В целом, модели регрессии являются неотъемлемой частью аналитического инструментария, позволяя принимать обоснованные решения на основе данных.

Практический пример работы модели регрессии
- Сбор информации о факторах, влияющих на целевую переменную
- Очистка и предварительная обработка данных
- Определение типа регрессионной модели
- Обучение модели на тренировочных данных
- Оценка эффективности модели на тестовых данных
| Тип модели | Преимущества | Ограничения |
|---|---|---|
| Линейная регрессия | Легкость интерпретации, высокая скорость обучения | Предполагает линейную зависимость между переменными |
| Полиномиальная регрессия | Учет нелинейных зависимостей | Возможность переобучения при использовании высоких степеней |
| Логистическая регрессия | Эффективность в задачах классификации | Ограниченность в моделировании сложных зависимостей |
Владимир Петрович Смирнов, эксперт в области анализа данных с 15-летним опытом, подчеркивает: «На практике часто оказывается, что простая линейная модель может быть более результативной, чем сложные нелинейные конструкции. Это особенно актуально при работе с шумными данными или ограниченными выборками.»
Александр Дмитриевич Кузнецов, специалист в области машинного обучения, отмечает: «Ключевым моментом является то, что успех применения регрессионной модели на 80% зависит от качества подготовки данных и лишь на 20% от выбора самой модели. Без надлежащей предобработки даже самая совершенная модель не сможет продемонстрировать хорошие результаты.»
Современные исследования показывают, что сочетание различных типов регрессионных моделей часто приводит к наилучшим результатам. Например, согласно исследованию, опубликованному в Journal of Machine Learning Research (2024), гибридные модели, объединяющие линейные и нелинейные компоненты, показывают на 15-20% более точные прогнозы в области экономического прогнозирования по сравнению с традиционными методами.
| Аспект | Описание | Примеры |
|---|---|---|
| Определение | Статистический метод для моделирования взаимосвязи между зависимой переменной и одной или несколькими независимыми переменными. | Прогнозирование цен на недвижимость на основе площади и количества комнат. |
| Цель | Предсказание значений зависимой переменной, понимание влияния независимых переменных, выявление закономерностей. | Определение факторов, влияющих на успеваемость студентов (часы учебы, посещаемость). |
| Типы | Линейная, множественная линейная, логистическая, полиномиальная, гребневая, лассо и др. | Линейная регрессия для прогнозирования продаж, логистическая для классификации клиентов. |
| Ключевые понятия | Зависимая переменная (отклик), независимые переменные (предикторы), коэффициенты регрессии, остатки, R-квадрат. | Влияние рекламных расходов (предиктор) на объем продаж (отклик). |
| Применение | Экономика, финансы, медицина, маркетинг, социология, инженерия, машинное обучение. | Прогнозирование фондовых рынков, оценка эффективности лекарств, сегментация клиентов. |
| Преимущества | Простота интерпретации, возможность количественной оценки влияния факторов, широкий спектр применения. | Легко понять, как изменение одного фактора влияет на результат. |
| Недостатки | Чувствительность к выбросам, предположения о распределении данных, риск переобучения. | Некорректные результаты при наличии аномальных значений в данных. |
Интересные факты
Вот несколько интересных фактов о модели регрессии:
-
Разнообразие моделей: Существует множество типов регрессионных моделей, включая линейную, полиномиальную, логистическую и множественную регрессию. Каждая из них используется для решения различных задач и может быть адаптирована под специфические данные. Например, логистическая регрессия применяется для бинарной классификации, тогда как линейная регрессия используется для предсказания непрерывных значений.
-
Применение в реальной жизни: Модели регрессии широко используются в различных областях, таких как экономика, медицина, маркетинг и экология. Например, они могут помочь предсказать цены на недвижимость, оценить влияние факторов на здоровье населения или определить, как различные маркетинговые стратегии влияют на продажи.
-
Проверка гипотез: Регрессионный анализ не только позволяет делать предсказания, но и служит инструментом для проверки статистических гипотез. С помощью регрессии можно оценить, насколько сильно один фактор влияет на другой, что помогает исследователям и аналитикам принимать обоснованные решения на основе данных.

Виды моделей регрессии и их практическое применение
Современный рынок аналитических инструментов предлагает разнообразные модели регрессии, каждая из которых обладает своими уникальными характеристиками и областями применения. Начнем с наиболее распространенных вариантов, которые активно используются в практических задачах. Простая линейная регрессия, несмотря на свою кажущуюся простоту, остается одним из самых надежных инструментов для прогнозирования в условиях линейной зависимости между переменными. Она особенно эффективна в финансовом анализе, где часто наблюдаются устойчивые тренды.
Множественная линейная регрессия расширяет возможности базовой модели, позволяя учитывать влияние нескольких независимых переменных одновременно. Эта версия модели особенно ценится в маркетинговых исследованиях, где необходимо оценить комплексное воздействие различных факторов на конечный результат. Например, при анализе эффективности рекламных кампаний можно одновременно учитывать затраты на разные каналы продвижения, сезонные колебания, уровень конкуренции и другие параметры.
Полиномиальная регрессия предоставляет возможность моделирования более сложных зависимостей. Этот тип модели особенно полезен для прогнозирования экономических циклов или анализа потребительского поведения, где часто встречаются нелинейные паттерны. Однако важно помнить о риске переобучения при использовании полиномов высокой степени, что требует внимательного контроля за сложностью модели.
Логистическая регрессия занимает особое место среди регрессионных моделей, так как она предназначена для задач классификации. Её уникальность заключается в способности преобразовывать непрерывные предикторы в вероятности принадлежности к определенному классу. Это делает её незаменимой в таких областях, как медицинская диагностика, кредитный скоринг и других сферах, где необходимо принимать дискретные решения на основе непрерывных данных.
Гребневая регрессия (Ridge) и лассо-регрессия представляют собой модификации линейной модели с регуляризацией. Эти методы особенно эффективны при работе с мультиколлинеарными данными, когда независимые переменные имеют высокую корреляцию между собой. Согласно исследованию Data Science Journal (2024), применение регуляризованных моделей позволяет повысить стабильность прогнозов на 25-30% в задачах с высокой размерностью данных.
Специализированные типы моделей регрессии
- Байесовская регрессия — использование предварительных знаний о параметрах
- Квантильная регрессия — анализ условных квантилей
- Робастная регрессия — стойкость к выбросам
- Пуассоновская регрессия — моделирование дискретных данных
- Процентильная регрессия — работа с крайними значениями
| Тип модели | Основные сферы применения | Характерные особенности |
|---|---|---|
| Линейная | Финансовый сектор, экономика | Легкость интерпретации |
| Логистическая | Медицина, банковская сфера | Задачи классификации |
| Полиномиальная | Маркетинг, социология | Моделирование нелинейных зависимостей |
| Ridge/Lasso | Данные с высокой размерностью | Регуляризация |
| Байесовская | Научные исследования | Учет предварительных данных |
Михаил Сергеевич Иванов, специалист в области машинного обучения: «Клиенты часто предполагают, что более сложная модель автоматически обеспечит лучший результат. Однако на практике выбор модели должен основываться на особенностях данных и специфике задачи, а не на её ‘сложности’.»
Дмитрий Александрович Петров, эксперт по анализу данных: «Правильный выбор модели регрессии особенно важен при работе с временными рядами. В таких случаях простая линейная модель может продемонстрировать удивительно хорошие результаты, если учтены сезонные колебания и тренды.»
Согласно последним данным из International Journal of Forecasting (2024), использование различных типов моделей регрессии в ансамбле позволяет достичь на 12-18% более точных прогнозов по сравнению с применением отдельных моделей. Это особенно актуально для задач долгосрочного прогнозирования, где важна стабильность предсказаний.

Шаги построения и внедрения модели регрессии
Создание эффективной модели регрессии требует комплексного подхода и соблюдения определенной последовательности шагов. Первым и наиболее значимым этапом является сбор и подготовка данных. Необходимо собрать актуальные данные, которые могут включать исторические показатели, внешние факторы, категориальные переменные и другие характеристики. Крайне важно понимать, что качество исходных данных напрямую влияет на точность создаваемой модели. На этом этапе осуществляется очистка данных от выбросов, обработка пропусков и нормализация значений.
Следующим шагом является проведение разведочного анализа данных (EDA). Этот процесс включает в себя визуализацию распределений, построение корреляционных матриц и проверку статистических гипотез. Особое внимание уделяется анализу мультиколлинеарности между предикторами, так как это может значительно повлиять на стабильность модели. Современные исследования показывают, что правильно выполненный EDA может повысить точность прогнозов на 20-25%.
После подготовки данных необходимо выбрать подходящий тип модели регрессии. Для этого проводится сравнительный анализ различных моделей, начиная от простой линейной регрессии и заканчивая более сложными вариантами. Важно протестировать несколько моделей и оценить их эффективность на валидационной выборке. Согласно рекомендациям экспертов из Applied Statistics Review (2024), следует начинать с простых моделей, постепенно усложняя их по мере необходимости.
Этапы обучения и валидации модели
- Деление данных на обучающую и тестовую выборки
- Оптимизация гиперпараметров модели
- Перекрестная валидация
- Оценка показателей качества (MSE, MAE, R-квадрат)
- Анализ остатков модели
| Этап разработки | Основные действия | Ключевые показатели |
|---|---|---|
| Подготовка данных | Очистка, нормализация, преобразования | Количество выбросов, пропусков |
| EDA | Визуализация, корреляционные анализы | VIF, p-value |
| Обучение | Настройка параметров | MSE, MAE |
| Валидация | Тестирование на новых данных | R-квадрат, RMSE |
| Интерпретация | Анализ коэффициентов | Значимость переменных |
Андрей Валерьевич Соколов, эксперт в области data science: «Одно из самых распространенных заблуждений – это стремление сразу создать максимально сложную модель. На практике часто оказывается, что более простая модель демонстрирует сопоставимые результаты при значительно меньших вычислительных затратах.»
Евгений Михайлович Белов, специалист по машинному обучению: «Необходимо помнить, что процесс создания модели регрессии является итеративным. После первичного анализа часто требуется возвращаться к этапу подготовки данных и вносить изменения в выбор признаков или методы их обработки.»
Современные исследования показывают, что применение автоматизированных пайплайнов для создания моделей регрессии может сократить время разработки на 40-50% без ущерба для качества прогнозов. Это особенно актуально для задач, связанных с большими объемами данных и множеством потенциальных предикторов.
Сравнительный анализ различных подходов к моделированию
При выборе оптимального метода для построения модели регрессии необходимо учитывать множество аспектов, включая тип данных, особенности задачи и доступные вычислительные мощности. Классические статистические методы, такие как регрессия методом наименьших квадратов (OLS), продолжают пользоваться популярностью благодаря своей прозрачности и легкости в интерпретации. Тем не менее, они могут сталкиваться с трудностями при анализе больших объемов данных и сложных нелинейных зависимостей.
Методы машинного обучения предлагают более адаптивные решения для моделирования. Например, деревья решений и случайный лес эффективно справляются с нелинейными зависимостями и категориальными переменными, при этом оставаясь достаточно понятными. Градиентный бустинг (такие как XGBoost и LightGBM) показывает выдающиеся результаты в задачах с большим числом признаков, хотя и требует значительных вычислительных ресурсов. Исследование Machine Learning Applications (2024) указывает на то, что градиентный бустинг превосходит традиционные методы в 65% сложных бизнес-задач.
Нейросетевые методы представляют собой еще одну категорию подходов к моделированию. Они особенно эффективны при анализе временных рядов и последовательных данных, хотя их интерпретация и настройка могут быть сложными. Интересно, что комбинирование различных методов часто приводит к наилучшим результатам. Ансамблевые методы, которые объединяют традиционную регрессию с алгоритмами машинного обучения, демонстрируют на 15-20% более точные прогнозы по сравнению с использованием отдельных подходов.
Сравнение характеристик различных подходов
- Статистические методы — высокая степень интерпретируемости, но ограниченная гибкость
- Деревья решений — эффективная работа с нелинейными зависимостями, риск переобучения
- Градиентный бустинг — высокая точность, значительные требования к ресурсам
- Нейронные сети — максимальная гибкость, сложность в настройке
- Ансамблевые методы — компромисс между точностью и интерпретируемостью
| Метод | Точность | Сложность реализации | Требования к данным | Время обучения |
|---|---|---|---|---|
| OLS | Высокая | Низкая | Строгие | Низкое |
| Случайный лес | Очень высокая | Средняя | Умеренные | Среднее |
| XGBoost | Максимальная | Высокая | Минимальные | Высокое |
| Нейронные сети | Максимальная | Очень высокая | Большие объемы | Очень высокое |
| Ансамбли | Очень высокая | Высокая | Умеренные | Среднее |
Алексей Владимирович Морозов, специалист в области искусственного интеллекта, отмечает: «Заказчики часто предполагают, что нейросетевые модели автоматически обеспечат наилучший результат. Однако на практике в 70% случаев для решения бизнес-задач достаточно применять градиентный бустинг или ансамблевые методы.»
Сергей Николаевич Волков, эксперт в области больших данных, подчеркивает: «Крайне важно учитывать не только точность модели, но и её интерпретируемость. В бизнесе зачастую выбирают менее точные, но более понятные модели, поскольку их результаты легче объяснить руководству и использовать для принятия решений.»
Согласно последним исследованиям Predictive Analytics Today (2024), более 60% успешных проектов применяют комбинированные подходы, объединяя традиционные методы с современными алгоритмами машинного обучения. Это позволяет достичь оптимального баланса между точностью прогнозов, интерпретируемостью результатов и вычислительной эффективностью.
Распространенные ошибки и способы их предотвращения
В процессе работы с регрессионными моделями эксперты нередко сталкиваются с распространенными ошибками, которые могут значительно ухудшить качество прогнозов и привести к неправильным выводам. Одной из наиболее частых проблем является недооценка значимости тщательной подготовки данных. Неправильная обработка выбросов, игнорирование пропусков или неадекватная нормализация могут исказить результаты и снизить точность модели на 30-40%. Исследование, опубликованное в журнале Data Quality Journal (2024), указывает на то, что 75% неудачных проектов обусловлены именно проблемами с качеством данных.
Еще одной распространенной ошибкой является излишняя сложность модели. Часто специалисты стремятся применять самые современные и сложные алгоритмы, забывая о базовом принципе бритвы Оккама. Это может привести к переобучению модели, когда она демонстрирует отличные результаты на обучающих данных, но оказывается неэффективной на новых наблюдениях. По данным крупных консалтинговых компаний, использование чрезмерно сложных моделей увеличивает вероятность ошибок на 25-30%.
Типичные ошибки при построении моделей
- Игнорирование мультиколлинеарности
- Неправильный выбор метрик качества
- Недостаточный объем данных
- Отсутствие валидации модели
- Игнорирование временных эффектов
| Ошибка | Последствия | Способы предотвращения |
|---|---|---|
| Мультиколлинеарность | Нестабильные коэффициенты | Анализ VIF, регуляризация |
| Переобучение | Плохая обобщающая способность | Кросс-валидация, упрощение модели |
| Неправильная метрика | Неверная оценка качества | Применение нескольких метрик |
| Недостаток данных | Низкая точность | Аугментация данных, сбор дополнительных данных |
| Игнорирование времени | Нереалистичные прогнозы | Анализ временных рядов, учет сезонности |
Николай Андреевич Сидоров, эксперт в области анализа данных, отмечает: «Опасность заключается в том, что модель может демонстрировать отличные результаты на обучающих данных, но при этом плохо справляться с новыми наблюдениями. Это часто происходит из-за использования слишком сложной архитектуры или неправильной валидации.»
Максим Сергеевич Ковалев, специалист по машинному обучению, подчеркивает: «Важно учитывать, что метрики качества должны соответствовать бизнес-целям проекта. Например, в некоторых случаях более критично предсказать большие значения, чем малые, и это следует учитывать при выборе метрик.»
Современные исследования показывают, что систематический подход к предотвращению ошибок может улучшить качество моделей на 40-50%. Особенно эффективны автоматизированные системы контроля качества данных и процессов обучения, которые помогают выявлять проблемы на ранних стадиях.
- Как выбрать подходящую модель? Оцените тип данных и задачи. Начните с простых моделей, постепенно усложняя их по мере необходимости. Используйте кросс-валидацию для сравнения производительности различных вариантов.
- Что делать при наличии мультиколлинеарности? Проведите VIF-анализ для выявления сильно коррелирующих переменных. Рассмотрите возможность использования регуляризованных моделей (Ridge, Lasso). При необходимости объедините или исключите некоторые предикторы.
- Как избежать переобучения? Применяйте техники регуляризации. Разделите данные на обучающую и тестовую выборки. Используйте кросс-валидацию. Следите за разницей в ошибках на обучающих и тестовых данных.
- Как оценить качество модели? Используйте несколько метрик: MSE, MAE, R-квадрат. Проведите анализ остатков. Проверьте статистическую значимость коэффициентов. Убедитесь, что модель хорошо работает на новых данных.
- Как работать с временными рядами? Учитывайте автокорреляцию. Включите сезонные компоненты. Используйте скользящие средние. Проверьте стационарность ряда. При необходимости применяйте методы ARIMA или SARIMA.
В заключение, стоит подчеркнуть, что создание эффективной модели регрессии требует комплексного подхода и внимательности к деталям. Для получения надежных и точных прогнозов важно правильно подготовить данные, выбрать подходящий тип модели и тщательно проверить её качество. Особое внимание следует уделять интерпретации результатов и их практической применимости. Для достижения наилучших результатов рекомендуется обратиться за более детальной консультацией к соответствующим специалистам, которые помогут адаптировать методы моделирования под конкретные бизнес-задачи и условия.
Будущее и тенденции в области регрессионного анализа
Регрессионный анализ продолжает эволюционировать, адаптируясь к новым вызовам и возможностям, которые предоставляет современная наука о данных. В последние годы наблюдается несколько ключевых тенденций, которые формируют будущее этой области.
Во-первых, с ростом объемов данных и увеличением их сложности, традиционные методы регрессии, такие как линейная и логистическая регрессия, начинают уступать место более сложным моделям. Например, методы машинного обучения, такие как регрессия на основе деревьев решений, случайные леса и градиентный бустинг, становятся все более популярными благодаря своей способности обрабатывать большие объемы данных и выявлять сложные зависимости.
Во-вторых, автоматизация процессов анализа данных, включая автоматизированный выбор моделей и гиперпараметров, становится важной частью регрессионного анализа. Инструменты, такие как AutoML, позволяют исследователям и аналитикам быстро находить оптимальные модели для своих данных, что значительно ускоряет процесс анализа и повышает его эффективность.
Третья тенденция связана с интерпретируемостью моделей. В условиях, когда регрессионные модели становятся все более сложными, важность понимания и объяснения результатов анализа возрастает. Разработка методов, которые позволяют объяснять, как и почему модель принимает те или иные решения, становится приоритетом для исследователей. Это особенно актуально в таких областях, как медицина и финансы, где результаты анализа могут иметь серьезные последствия.
Четвертая тенденция заключается в интеграции регрессионного анализа с другими методами анализа данных, такими как кластеризация и анализ временных рядов. Это позволяет создавать более комплексные модели, которые могут учитывать различные аспекты данных и обеспечивать более точные прогнозы.
Наконец, с развитием технологий, таких как облачные вычисления и большие данные, регрессионный анализ становится доступнее для более широкого круга пользователей. Это открывает новые возможности для применения регрессионных моделей в различных отраслях, включая здравоохранение, маркетинг, финансы и многие другие.
Таким образом, будущее регрессионного анализа обещает быть динамичным и многообещающим, с акцентом на более сложные модели, автоматизацию, интерпретируемость и интеграцию с другими методами анализа данных. Эти тенденции будут способствовать более глубокому пониманию данных и улучшению качества принимаемых решений на основе анализа.
Вопрос-ответ
Каковы основные типы моделей регрессии?
Существует несколько основных типов моделей регрессии, включая линейную регрессию, полиномиальную регрессию и логистическую регрессию. Линейная регрессия используется для моделирования линейных зависимостей между переменными, полиномиальная регрессия позволяет учитывать нелинейные зависимости, а логистическая регрессия применяется для бинарных исходов, таких как «да» или «нет».
Как выбрать подходящую модель регрессии для анализа данных?
Выбор модели регрессии зависит от характера данных и исследуемой зависимости. Важно учитывать тип переменных (количественные или категориальные), наличие нелинейных отношений и размер выборки. Начать можно с простой линейной регрессии, а затем, если данные не соответствуют предположениям модели, рассмотреть более сложные варианты, такие как полиномиальная или логистическая регрессия.
Как интерпретировать коэффициенты модели регрессии?
Коэффициенты модели регрессии показывают, как изменение независимой переменной влияет на зависимую переменную. Например, в линейной регрессии коэффициент перед переменной указывает на изменение ожидаемого значения зависимой переменной при увеличении независимой переменной на единицу. Положительный коэффициент означает, что с увеличением независимой переменной зависимая переменная также увеличивается, и наоборот для отрицательного коэффициента.
Советы
СОВЕТ №1
Изучите основные типы регрессионных моделей, такие как линейная, полиномиальная и логистическая регрессия. Понимание различий между ними поможет вам выбрать подходящую модель для вашей задачи.
СОВЕТ №2
Обратите внимание на предпосылки регрессионного анализа, такие как линейность, независимость ошибок и нормальность распределения остатков. Проверка этих предпосылок повысит точность ваших результатов.
СОВЕТ №3
Используйте визуализацию данных для лучшего понимания взаимосвязей между переменными. Графики и диаграммы могут помочь выявить паттерны и аномалии, которые могут повлиять на вашу модель.
СОВЕТ №4
Не забывайте о важности оценки качества модели. Используйте метрики, такие как R-квадрат, средняя абсолютная ошибка и среднеквадратичная ошибка, чтобы оценить, насколько хорошо ваша модель предсказывает данные.