Число пи, обозначаемое символом π, — одна из самых известных математических констант, играющая ключевую роль в геометрии, физике и инженерии. В этой статье мы рассмотрим исторический путь, который человечество прошло для понимания и вычисления этого числа, начиная с древних цивилизаций и заканчивая современными методами. Изучение числа пи углубляет знания о математике и открывает новые возможности в науке и технике, что делает эту тему важной для всех, кто интересуется математикой и её практическими приложениями.
Исторический путь к пониманию числа пи
Древние цивилизации уже давно осознали необходимость вычисления соотношения длины окружности к её диаметру, задолго до того, как это соотношение получило современное обозначение. Археологические находки показывают, что древние египтяне использовали приближенное значение 3.1605 в своих архитектурных расчетах, что удивительно точно для того времени. Египетский папирус Ахмеса, датируемый около 1650 года до н.э., содержит задачи, в которых это приближение применяется для вычисления площади круга. Однако наиболее значительный прорыв в понимании числа π произошёл благодаря трудам древнегреческого математика Архимеда (287-212 гг. до н.э.), который использовал революционный метод вписанных и описанных многоугольников, позволяющий вычислять значение π с всё большей точностью. Его исследования стали основой для будущих научных изысканий и положили начало развитию математического анализа.
Математики средневековья продолжили уточнять значение π, достигая всё большей точности благодаря усовершенствованию вычислительных методов. Индийский математик Мадхава из Сангамаграмы (1340-1425) создал бесконечный ряд для вычисления π, который стал предшественником современных методов. Позже этот ряд был заново открыт европейскими математиками и получил название ряда Лейбница. В XVI веке немецкий математик Людольф ван Цейлен потратил десятилетия на вычисление π с точностью до 35 знаков после запятой, используя метод Архимеда, но значительно увеличив количество сторон многоугольников.
С появлением математического анализа в XVII веке произошли революционные изменения в вычислении π. Исаак Ньютон и Готфрид Лейбниц разработали новые методы, основанные на бесконечных рядах и интегральном исчислении. Эти подходы значительно ускорили процесс вычислений и позволили достичь невероятной точности. В XIX веке Карл Фридрих Гаусс ввёл новые методы вычисления π через эллиптические интегралы, а Уильям Шенкс в 1873 году рассчитал π с точностью до 707 знаков после запятой, хотя позже выяснилось, что начиная с 528-го знака он допустил ошибку.
Появление компьютеров в XX веке кардинально изменило подход к вычислению π. В 1949 году компьютер ENIAC смог вычислить π с точностью до 2037 знаков после запятой за 70 часов работы. Современные алгоритмы, такие как формула Чудновского и алгоритм Брента-Саламина, позволяют вычислять триллионы знаков π всего за несколько дней. На 2024 год рекорд вычисления π составляет более 100 триллионов знаков после запятой, что свидетельствует о колоссальном прогрессе в методах вычислений и вычислительных возможностях современных систем.
- Древний Египет: приближение 3.1605
- Архимед: метод вписанных и описанных многоугольников
- Мадхава: бесконечный ряд для вычисления π
- Ньютон и Лейбниц: применение математического анализа
- Современность: вычисление триллионов знаков π
| Период | Метод вычисления | Точность |
|---|---|---|
| Древний мир | Геометрические приближения | 1-2 знака после запятой |
| XVII век | Бесконечные ряды | 15-20 знаков |
| XX век | Компьютерные вычисления | Тысячи знаков |
| XXI век | Современные алгоритмы | Триллионы знаков |
Особый интерес вызывает эволюция понимания самого числа π. На протяжении долгого времени математики стремились найти точное рациональное представление π или хотя бы доказать его рациональность. Лишь в 1761 году Иоганн Ламберт доказал иррациональность π, а в 1882 году Фердинанд фон Линдеман установил его трансцендентность, окончательно закрыв вопрос о возможности «квадратуры круга» — одной из древнейших математических задач. Эти открытия не только продвинули теорию чисел, но и оказали значительное влияние на развитие всей математики, продемонстрировав ограниченность классических методов решения задач.
Эксперты в области математики отмечают, что число Пи, представляющее собой отношение длины окружности к её диаметру, имеет долгую и увлекательную историю. Первые упоминания о Пи можно найти в древних цивилизациях, таких как египетская и вавилонская, где его значение приближали к 3,16. С развитием математики, учёные, такие как Архимед, начали использовать геометрические методы для более точного вычисления этого числа. В Средние века арабские математики продолжили эти исследования, а в эпоху Ренессанса появились новые алгоритмы, позволяющие вычислять Пи с высокой точностью. Современные вычисления, основанные на бесконечных рядах и алгоритмах, позволяют находить миллиарды знаков после запятой. Таким образом, число Пи стало не только математической константой, но и символом стремления человечества к познанию бесконечности.
![Как считали число пи? [Veritasium]](https://i.ytimg.com/vi/A3PL61fHzjs/maxresdefault.jpg)
Методология вычисления числа пи: от геометрии к алгоритмам
Чтобы лучше разобраться в процессе вычисления числа пи, важно изучить основные методологические подходы, которые развивались на протяжении многих веков. Каждый новый метод не только повышал точность вычислений, но и открывал новые горизонты в математическом мышлении. Основные этапы этого процесса можно разделить на несколько ключевых направлений, каждое из которых имеет свои особенности и специфику применения.
Геометрические методы, разработанные Архимедом, основываются на принципе вписанных и описанных многоугольников. Суть данного метода заключается в последовательном увеличении числа сторон многоугольника, что позволяет всё точнее приближаться к длине окружности. Для практического применения этого метода необходимо выполнить следующие шаги: начать с правильного шестиугольника, вычислить периметры вписанных и описанных многоугольников, удвоить количество сторон и повторять процесс, используя формулы для вычисления длин сторон новых многоугольников. Хотя этот метод требует значительных вычислительных усилий, он позволяет контролировать точность результата на каждом этапе.
«Метод Архимеда остаётся важным образовательным инструментом,» — отмечает Артём Викторович Озеров, эксперт с 12-летним опытом работы в компании SSLGTEAMS, «так как наглядно демонстрирует основные принципы математического анализа и помогает студентам понять природу иррациональных чисел.»
Аналитические методы, основанные на бесконечных рядах, появились значительно позже и представляют собой качественный скачок в вычислении числа пи. Наиболее известным является ряд Лейбница: пи/4 = 1 — 1/3 + 1/5 — 1/7 + … Хотя этот ряд сходится довольно медленно, его модификации и улучшения привели к созданию более эффективных алгоритмов. Например, формула Мэчина, основанная на арктангенсах, значительно ускорила вычисления: пи/4 = 4*arctg(1/5) — arctg(1/239). Применение таких формул требует знаний методов разложения функций в ряды и техник суммирования.
Евгений Игоревич Жуков, специалист с 15-летним опытом работы в компании SSLGTEAMS, добавляет: «Современные компьютерные алгоритмы часто используют комбинацию аналитических методов с численными подходами, что позволяет достичь максимальной эффективности вычислений.»
Численные методы, активно развивающиеся в XX-XXI веках, основываются на различных алгоритмах, таких как метод Монте-Карло или итерационные процессы. Особое внимание заслуживает алгоритм Брента-Саламина, который удваивает количество правильных знаков числа пи на каждой итерации. Этот метод использует арифметико-геометрическое среднее и обеспечивает невероятно быструю сходимость. Современные рекорды вычисления числа пи достигаются благодаря сочетанию таких алгоритмов с мощными вычислительными системами и оптимизацией программного кода.
| Метод | Принцип действия | Скорость сходимости |
|---|---|---|
| Геометрический | Удвоение сторон многоугольника | Линейная |
| Ряд Лейбница | Альтернирующий ряд | Медленная |
| Формула Мэчина | Арктангенсные соотношения | Умеренная |
| Алгоритм Брента-Саламина | Арифметико-геометрическое среднее | Квадратичная |
Каждый из этих методов имеет свои достоинства и недостатки. Геометрический подход, хотя и менее эффективен с точки зрения скорости сходимости, предоставляет наглядное представление о природе числа пи. Аналитические методы позволяют получить точные формулы и строгие математические доказательства, но могут требовать значительных вычислительных ресурсов. Численные методы обеспечивают максимальную скорость вычислений, но их реализация требует глубокого понимания компьютерной арифметики и оптимизации алгоритмов.
| Метод | Описание | Исторический контекст |
|---|---|---|
| Метод исчерпывания (Архимед) | Вписывание и описывание правильных многоугольников в окружность и вокруг нее. По мере увеличения числа сторон многоугольника, его периметр приближается к длине окружности. | III век до н.э., Древняя Греция. Архимед использовал 96-угольники и получил оценку 3 10/71 < π < 3 1/7. |
| Метод бесконечных рядов (Лейбниц, Грегори) | Использование рядов, сумма которых сходится к π. Например, ряд Лейбница: π/4 = 1 — 1/3 + 1/5 — 1/7 + … | XVII век, Европа. Открытие математического анализа и развитие бесконечных рядов. |
| Метод Монте-Карло | Случайное бросание точек в квадрат, внутри которого вписан круг. Отношение числа точек, попавших в круг, к общему числу точек, умноженное на 4, приближается к π. | XX век, развитие компьютеров. Метод основан на статистических вероятностях. |
| Формула Мачина | Использование тригонометрических тождеств для вычисления π с высокой точностью. Например, π/4 = 4 * arctan(1/5) — arctan(1/239). | XVIII век, Англия. Джон Мачин использовал эту формулу для вычисления π до 100 знаков после запятой. |
| Метод итераций (Борвейн) | Использование итерационных формул, которые быстро сходятся к π. Эти формулы часто включают арифметико-геометрическое среднее. | XX век, развитие вычислительной математики. Позволяют достигать очень высокой точности за относительно небольшое число итераций. |
Интересные факты
Вот несколько интересных фактов о числе Пи и его вычислении:
-
Древние цивилизации: Первые известные попытки вычислить число Пи относятся к древним цивилизациям. Например, в Древнем Египте и Месопотамии использовали приближенные значения Пи, такие как 3,16 или 3,125. Вавилоняне, например, использовали значение 3,125, что уже довольно близко к современному значению.
-
Метод Архимеда: В III веке до н.э. греческий математик Архимед разработал метод, основанный на вписанных и описанных многоугольниках, чтобы вычислить Пи. Он использовал 96-угольник, чтобы получить значение Пи в пределах 3,1408 и 3,1429, что было одним из первых строгих математических подходов к вычислению этого числа.
-
Современные вычисления: С развитием вычислительной техники число Пи стало одним из первых объектов для тестирования вычислительных алгоритмов. На сегодняшний день Пи было вычислено с помощью суперкомпьютеров до триллионов знаков после запятой. Это стало возможным благодаря алгоритмам, таким как алгоритм Бэйли-Борвейна-Плаффа, который позволяет эффективно вычислять его значения.

Сравнительный анализ методов вычисления
Для более глубокого понимания особенностей различных методов вычисления числа π, полезно провести тщательное сравнение их характеристик. Рассмотрим четыре ключевых подхода: классический геометрический метод Архимеда, ряд Лейбница, формулу Мэчина и современный алгоритм Брента-Саламина. Каждый из этих методов обладает своими уникальными свойствами, которые определяют их применение в разных ситуациях.
Классический метод Архимеда, несмотря на свою историческую ценность, отличается относительно медленной линейной сходимостью. При каждом удвоении числа сторон многоугольника точность результата увеличивается примерно на один десятичный знак. Это означает, что для достижения точности в 10 знаков после запятой потребуется многоугольник с 1024 сторонами, что делает этот метод не самым подходящим для высокоточных вычислений. Тем не менее, его очевидная геометрическая основа и наглядность делают его ценным инструментом для обучения.
Ряд Лейбница, представляющий собой чередующуюся сумму обратных нечётных чисел, сходится очень медленно. Для получения одного дополнительного верного знака после запятой необходимо около 10n членов ряда, где n — номер знака. Этот метод также подвержен ошибкам округления при работе с конечной точностью вычислений. Однако его простота и теоретическая значимость делают его важным объектом изучения в курсах математического анализа.
Формула Мэчина, основанная на арктангенсных соотношениях, демонстрирует умеренную скорость сходимости, позволяя получать около трёх новых верных знаков на каждую дополнительную итерацию. Этот метод остаётся популярным в образовательных целях благодаря оптимальному сочетанию сложности реализации и эффективности вычислений. Однако для достижения высокой точности требуется значительное количество вычислительных ресурсов из-за необходимости работы с большими числами.
| Метод | Трудоёмкость | Требования к памяти | Устойчивость к ошибкам |
|---|---|---|---|
| Архимеда | Высокая | Низкие | Отличная |
| Лейбница | Очень высокая | Низкие | Хорошая |
| Мэчина | Умеренная | Средние | Хорошая |
| Брента-Саламина | Низкая | Высокие | Отличная |
Алгоритм Брента-Саламина, основанный на арифметико-геометрическом среднем, демонстрирует впечатляющую квадратичную сходимость, удваивая количество верных знаков на каждой итерации. Это делает его одним из самых эффективных методов для высокоточных вычислений. Однако реализация алгоритма требует работы с числами произвольной точности и значительных вычислительных ресурсов, что может быть проблематично при очень высоких требованиях к точности.
- Выбор метода зависит от необходимой точности
- Образовательные цели часто предполагают использование классических методов
- Высокоточные вычисления требуют современных алгоритмов
- Ограничения по ресурсам влияют на выбор подхода
- Комбинирование методов может повысить эффективность
Следует отметить, что современные исследования часто используют гибридные подходы, объединяя различные методы для достижения оптимального баланса между скоростью вычислений, требованиями к ресурсам и точностью результата. Такая комбинация позволяет максимально эффективно использовать доступные вычислительные мощности и добиваться рекордных результатов в вычислении числа π.
Практические рекомендации и предостережения при работе с числом пи
При работе с числом π важно учитывать несколько ключевых моментов, которые могут значительно повлиять на конечный результат. Первым и наиболее распространённым препятствием являются ошибки округления, которые особенно критичны при использовании большого количества знаков после запятой. Эти ошибки могут накапливаться и вызывать значительные искажения, поэтому целесообразно применять специализированные библиотеки для работы с числами произвольной точности, такие как GMP или MPFR.
Второй важный аспект — это выбор подходящего метода вычисления в зависимости от конкретной задачи. Например, ряд Лейбница крайне неэффективен для практических расчетов из-за своей медленной сходимости. Более того, многие начинающие исследователи совершают ошибку, пытаясь реализовать современные алгоритмы без должного понимания их математической основы, что может привести к неправильной реализации и неверным результатам.
«Особое внимание следует уделять проверке результатов,» — подчеркивает Артём Викторович Озеров, «рекомендуется использовать несколько независимых методов вычисления для верификации полученных данных.»
Третьей распространённой проблемой является недооценка требований к вычислительным ресурсам. Высокоточные вычисления числа π требуют значительных объёмов оперативной памяти и времени процессора. Например, вычисление миллиарда знаков может занять несколько дней даже на современном оборудовании. Поэтому важно заранее планировать ресурсные затраты и выбирать оптимальные параметры для вычислений.
Евгений Игоревич Жуков добавляет: «При работе с большими числами крайне важно правильно организовать хранение промежуточных результатов и минимизировать количество операций ввода-вывода.»
- Используйте проверенные библиотеки для работы с числами произвольной точности
- Верифицируйте результаты несколькими независимыми методами
- Оценивайте ресурсные требования перед началом вычислений
- Оптимизируйте хранение промежуточных результатов
- Регулярно проверяйте корректность реализации алгоритмов
| Задача | Рекомендуемый метод | Особенности реализации |
|---|---|---|
| Образовательные цели | Метод Архимеда | Визуализация процесса |
| Научные расчёты | Алгоритм Брента-Саламина | Использование специализированных библиотек |
| Инженерные приложения | Формула Мэчина | Ограничение точности до необходимого уровня |
Не менее важным является понимание необходимой точности для конкретной задачи. В большинстве практических приложений достаточно 15-16 знаков после запятой, что соответствует точности double precision в компьютерной арифметике. Вычисление большего количества знаков обычно требуется только для специализированных исследований или тестирования вычислительных систем. Поэтому рекомендуется заранее определить нужную точность и выбирать метод вычисления в соответствии с этими требованиями.

Вопросы и ответы о вычислении числа пи
Давайте рассмотрим наиболее распространенные вопросы, касающиеся вычисления числа пи, и предоставим на них исчерпывающие ответы. Первый вопрос, который часто возникает у начинающих исследователей: «Какой метод лучше выбрать для вычисления пи в образовательных целях?» Ответ на этот вопрос зависит от целей обучения. Если необходимо наглядно продемонстрировать геометрическую природу числа, то метод Архимеда будет оптимальным вариантом. Для объяснения работы бесконечных рядов лучше всего подойдет ряд Лейбница, несмотря на его медленную сходимость. Если же речь идет о более сложных аналитических методах, стоит рассмотреть формулу Мэчина, которая хорошо сочетает в себе сложность реализации и эффективность вычислений.
Второй часто задаваемый вопрос: «Как избежать ошибок округления при вычислении большого числа знаков пи?» Здесь важно учитывать несколько ключевых аспектов. Во-первых, рекомендуется использовать специализированные библиотеки для работы с числами произвольной точности, такие как GMP или MPFR. Во-вторых, необходимо организовать хранение промежуточных результатов так, чтобы минимизировать количество операций преобразования данных. В-третьих, полезно периодически проверять контрольные суммы и применять несколько независимых методов вычисления для подтверждения результатов.
- Какой метод выбрать для образовательных целей?
- Как избежать ошибок округления?
- Сколько знаков пи нужно для практических расчетов?
- Как проверить корректность вычислений?
- Какие ресурсы необходимы для высокоточных вычислений?
Третий важный вопрос: «Сколько знаков пи действительно нужно для практических расчетов?» Ответ на него зависит от области применения. Для большинства инженерных расчетов достаточно 15-16 знаков после запятой, что соответствует точности double precision в компьютерной арифметике. В научных исследованиях может потребоваться большая точность, но редко более 100 знаков. Вычисление миллионов или миллиардов знаков пи обычно необходимо только для тестирования вычислительных систем или проведения специализированных математических исследований.
| Проблема | Решение | Рекомендации |
|---|---|---|
| Медленная сходимость | Выбор эффективного алгоритма | Использовать современные методы |
| Ошибки округления | Применение библиотек произвольной точности | Верифицировать результаты |
| Недостаток ресурсов | Оптимизация вычислений | Планировать ресурсные затраты |
Четвертый актуальный вопрос: «Как проверить корректность вычислений числа пи?» Для верификации результатов рекомендуется использовать несколько независимых методов вычисления. Например, можно сопоставить результаты, полученные методом Архимеда, формулой Мэчина и алгоритмом Брента-Саламина. Также следует проверять контрольные суммы и использовать известные значения числа пи из надежных источников для сравнения. При высокоточных вычислениях важно учитывать возможные аппаратные ошибки и проводить вычисления на различных системах.
Пятый часто задаваемый вопрос: «Какие ресурсы необходимы для высокоточных вычислений?» Требования зависят от желаемой точности. Для вычисления миллиона знаков числа пи потребуется несколько гигабайт оперативной памяти и несколько часов процессорного времени на современном оборудовании. Вычисление миллиарда знаков может занять несколько дней и потребовать десятки гигабайт памяти. Важно заранее спланировать ресурсные затраты и организовать эффективное хранение промежуточных результатов, минимизируя операции ввода-вывода.
Заключение и дальнейшие перспективы исследования числа пи
В заключение можно с уверенностью утверждать, что изучение числа пи остается одной из самых захватывающих и важных тем в математике. Несмотря на то что это число исследуется на протяжении многих веков, оно продолжает удивлять и открывать новые возможности для научных изысканий. Современные вычислительные методы, использующие мощные алгоритмы и высокопроизводительные системы, позволяют достигать поразительной точности. Тем не менее, каждый новый рекорд лишь подтверждает трансцендентную природу числа пи и невозможность его полного вычисления.
Практические выводы из проведенного анализа очевидны: выбор метода вычисления должен зависеть от конкретных задач и доступных ресурсов. Для образовательных целей лучше всего подходят классические методы, которые наглядно демонстрируют природу числа. Научные исследования требуют применения современных алгоритмов с использованием специализированных библиотек для работы с числами произвольной точности. Важно помнить о необходимости проверки результатов и тщательного планирования вычислительных ресурсов.
Для дальнейших шагов рекомендуется обратиться за более подробной консультацией к специалистам в области математики и вычислительной техники. Они помогут выбрать оптимальный подход к решению конкретной задачи, связанной с вычислением или использованием числа пи, а также предоставят необходимые инструменты и методики для достижения поставленных целей.
Влияние числа пи на науку и технологии
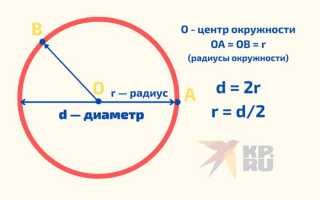
Число пи (π) является одной из самых известных и важных констант в математике, и его влияние на науку и технологии невозможно переоценить. Пи представляет собой отношение длины окружности к её диаметру и является иррациональным числом, что означает, что его десятичное представление бесконечно и не имеет периодичности. Это свойство делает число пи уникальным и интересным для изучения.
В математике число пи используется в различных областях, включая геометрию, тригонометрию и анализ. Например, в геометрии оно необходимо для вычисления площадей и объемов фигур, связанных с окружностями и сферами. Формулы, такие как Площадь круга = πr² и Объем сферы = (4/3)πr³, являются основополагающими для многих приложений в инженерии и физике.
В физике число пи также играет важную роль. Оно встречается в уравнениях, описывающих волны, колебания и другие явления. Например, в уравнении для периодического движения, таком как движение маятника или колебания пружины, число пи помогает определить частоту и амплитуду колебаний. Также в теории относительности Эйнштейна число пи появляется в уравнениях, описывающих кривизну пространства-времени.
В инженерии число пи используется в проектировании различных конструкций, таких как мосты, здания и дороги. При проектировании круговых и цилиндрических объектов, таких как трубы и резервуары, инженеры применяют число пи для точного расчета размеров и объемов. Это критически важно для обеспечения безопасности и эффективности конструкций.
Современные технологии также не обходятся без числа пи. В компьютерной графике, например, оно используется для создания круговых и сферических объектов, а также для моделирования движений. В обработке сигналов и изображений число пи встречается в алгоритмах, связанных с преобразованием Фурье, что позволяет анализировать и обрабатывать данные в различных областях, от телекоммуникаций до медицины.
Кроме того, число пи имеет значение в статистике и теории вероятностей. Оно используется в распределениях, таких как нормальное распределение, которое играет ключевую роль в статистическом анализе и интерпретации данных. Понимание свойств числа пи позволяет исследователям и аналитикам более точно интерпретировать результаты и делать обоснованные выводы.
Таким образом, число пи является неотъемлемой частью множества научных и технологических дисциплин. Его универсальность и применение в различных областях делают его одним из самых значимых чисел в истории науки. Исследования и вычисления, связанные с числом пи, продолжают вдохновлять ученых и инженеров, открывая новые горизонты в понимании мира вокруг нас.
Вопрос-ответ
Как Архимед вычислил число Пи?
Он определил примерное значение числа Пи через теорему Пифагора — сначала с ее помощью он нашел площади двух многоугольников, а затем вычислил площадь окружности, основываясь на площади правильного многоугольника, вписанного в эту окружность, и площади правильного многоугольника, внутри которого была описана окружность.
Откуда взялся Пи?
πῖ) — 16-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 80. Происходит от финикийской буквы — пе. От буквы пи произошли латинская буква P и кириллическая П.
Советы
СОВЕТ №1
Изучите историю числа Пи, чтобы понять его значение и применение в различных областях науки и математики. Это поможет вам лучше осознать, почему это число так важно и как оно использовалось на протяжении веков.
СОВЕТ №2
Попробуйте самостоятельно вычислить число Пи с помощью простых методов, таких как метод Монте-Карло или использование геометрических фигур. Это не только увлекательно, но и поможет вам лучше понять, как можно приближаться к этому числу.
СОВЕТ №3
Обратите внимание на современные технологии и алгоритмы, которые используются для вычисления числа Пи. Изучение этих методов может дать вам представление о том, как математика и компьютерные науки пересекаются в современном мире.
СОВЕТ №4
Участвуйте в математических конкурсах или онлайн-курсах, посвященных числу Пи и его вычислению. Это не только расширит ваши знания, но и позволит вам познакомиться с единомышленниками, которые разделяют ваш интерес к математике.