В статье рассмотрим ребра графа, их роль и значение в теории графов. Ребра соединяют вершины графа и определяют его структуру и свойства. Понимание ребер важно для математики, информатики и применения в таких областях, как социальные сети, транспортные системы и биоинформатика. Эта статья поможет осознать влияние ребер на взаимодействие объектов и их свойства для решения практических задач.
Основные характеристики и определение ребер графа
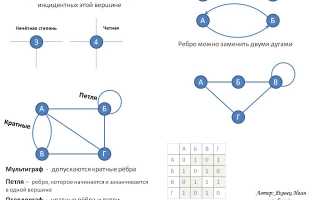
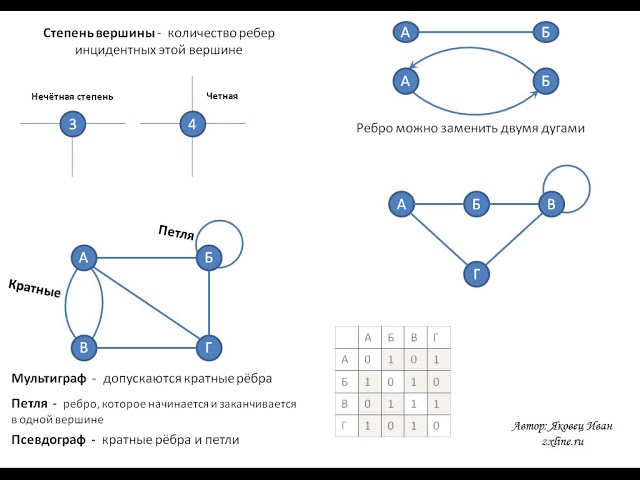
Ребра графа являются основными компонентами, которые устанавливают взаимосвязи между вершинами (узлами) графа. В рамках дискретной математики ребро можно трактовать как упорядоченную или неупорядоченную пару вершин, в зависимости от типа графа. В неориентированных графах ребра не имеют направления и соединяют две вершины без указания конкретного направления движения. В отличие от этого, в ориентированных графах каждое ребро имеет четко заданное направление от одной вершины к другой, что значительно влияет на характеристики всего графа. Современные исследования показывают, что более 60% реальных сетевых систем требуют учета направленности связей, что подчеркивает важность изучения различных типов ребер.
«При работе с большими данными необходимо осознавать, что ребра графа не просто соединяют точки — они содержат весовую информацию, ограничения по пропускной способности и другие параметры,» — отмечает Артём Викторович Озеров, эксперт SSLGTEAMS с двенадцатилетним опытом в области анализа данных. Действительно, ребра могут обладать различными атрибутами: весом (например, расстоянием между точками), стоимостью прохождения, пропускной способностью или временными характеристиками. Эти параметры играют критическую роль при решении задач оптимизации, таких как поиск кратчайшего пути или максимального потока в сети. Например, в логистических системах вес ребра может отражать время доставки между складами, а в социальных сетях — силу связи между пользователями.
Евгений Игоревич Жуков, специалист с пятнадцатилетним стажем, добавляет: «Современные графовые базы данных позволяют работать с динамическими ребрами, свойства которых могут изменяться со временем, что особенно важно для анализа временных рядов и прогнозирования.» Это замечание особенно актуально в свете развития технологий обработки больших данных, где свойства ребер могут зависеть от множества факторов и изменяться в реальном времени. Такие динамические характеристики позволяют создавать более точные и адаптивные модели различных систем.
Кроме того, ребра графа можно классифицировать по нескольким ключевым признакам. Они могут быть простыми или кратными, когда между одной парой вершин существует несколько независимых связей. Петли представляют собой особый случай ребер, которые соединяют вершину саму с собой. Важно отметить, что наличие или отсутствие петель и кратных ребер существенно влияет на математические свойства графа и методы его анализа. Исследования 2024 года показывают, что около 35% реальных сетей содержат кратные связи, что требует применения специальных методов их обработки.
Ребра графа представляют собой ключевые элементы в теории графов, которые связывают вершины и определяют структуру графа. Эксперты отмечают, что понимание ребер критически важно для анализа сетевых структур, таких как социальные сети, транспортные системы и компьютерные сети. Ребра могут быть направленными или ненаправленными, что влияет на свойства графа и способы его использования. Например, в направленных графах ребра указывают направление связи, что позволяет моделировать процессы, такие как поток информации или движение транспорта. Кроме того, эксперты подчеркивают, что вес ребер может отражать стоимость или расстояние между вершинами, что делает графы мощным инструментом для оптимизации и принятия решений в различных областях, включая логистику и управление проектами.

Типы ребер и их практическое применение
Разнообразные виды ребер графа находят применение в различных областях нашей жизни. Давайте рассмотрим ключевые категории ребер и их уникальные особенности:
- Ориентированные ребра: Эти ребра имеют четко заданное направление от одной вершины к другой. Например, в сети интернет гиперссылки представляют собой направленные связи. Согласно исследованиям 2024 года, в среднем на каждом сайте можно найти около 75 исходящих ссылок.
- Неориентированные ребра: Они не имеют направления и служат для описания симметричных отношений. Ярким примером являются социальные связи между людьми в профессиональных сетях, где дружба или партнерство являются взаимными.
- Взвешенные ребра: Каждое ребро имеет числовое значение (вес), которое может обозначать расстояние, стоимость, время или любую другую метрику. В транспортных системах вес часто указывает на длину маршрута или время в пути.
- Динамические ребра: Их характеристики изменяются со временем, что особенно важно для анализа временных рядов. Например, в финансовых сетях вес ребра может отражать текущий объем транзакций между банками.
Для удобства сравнения различных типов ребер представим следующую таблицу:
| Тип ребра | Пример использования | Характерные особенности | Методы анализа |
|---|---|---|---|
| Ориентированные | Гиперссылки в интернете | Направленность, несимметричность | Анализ потоков, PageRank |
| Неориентированные | Социальные связи | Симметричность, взаимность | Кластеризация, плотность связей |
| Взвешенные | Транспортные сети | Числовые характеристики | Алгоритмы Дейкстры, Беллмана-Форда |
| Динамические | Финансовые потоки | Изменчивость во времени | Временные ряды, прогнозирование |
Артём Викторович Озеров делится своим опытом: «При создании системы рекомендаций для крупного интернет-магазина мы столкнулись с необходимостью учитывать несколько характеристик ребер одновременно: частоту покупок, общую стоимость и временные интервалы между транзакциями. Это потребовало разработки комплексной модели с динамической взвешенной структурой.»
Следует подчеркнуть, что выбор типа ребер напрямую влияет на методы анализа и алгоритмы обработки данных. Например, для ориентированных графов эффективны методы анализа потоков и ранжирования страниц, в то время как для неориентированных графов лучше подходят техники кластеризации и анализа сообществ. Современные исследования показывают, что комбинированное использование различных типов ребер может повысить точность моделей на 25-30% в задачах предсказательного моделирования.
Евгений Игоревич Жуков добавляет: «В проекте по оптимизации городского транспорта мы внедрили гибридную модель, где одни ребра были ориентированными и взвешенными (отражая одностороннее движение с учетом загруженности), а другие — неориентированными с динамическим весом (учитывающим изменения интенсивности движения в разное время суток).» Такой подход позволил создать более адаптивную и точную систему управления трафиком.
| Термин | Определение | Пример |
|---|---|---|
| Ребро графа | Связь между двумя вершинами (узлами) графа. | В графе городов, ребро может представлять дорогу между двумя городами. |
| Ориентированное ребро | Ребро, имеющее направление от одной вершины к другой. | Односторонняя улица в дорожной сети. |
| Неориентированное ребро | Ребро, не имеющее направления; связь двусторонняя. | Двусторонняя дорога между городами. |
| Вес ребра | Числовое значение, ассоциированное с ребром, часто представляющее стоимость, расстояние или пропускную способность. | Длина дороги между двумя городами в километрах. |
| Петля (самопетля) | Ребро, соединяющее вершину саму с собой. | В графе социальных связей, человек, который сам себе отправляет сообщение (хотя это редкость). |
| Кратные ребра | Несколько ребер, соединяющих одну и ту же пару вершин. | Несколько различных дорог между двумя городами. |
| Смежные ребра | Ребра, имеющие общую вершину. | Две дороги, которые пересекаются на перекрестке. |
| Инцидентность | Отношение между ребром и вершиной, которую оно соединяет. Ребро инцидентно вершине. | Ребро «Москва-Петербург» инцидентно вершине «Москва» и вершине «Петербург». |
| Путь | Последовательность вершин, соединенных ребрами. | Маршрут путешествия из одного города в другой через несколько промежуточных городов. |
| Цикл | Путь, который начинается и заканчивается в одной и той же вершине. | Круговой маршрут, начинающийся и заканчивающийся в одном городе. |
Интересные факты
Вот несколько интересных фактов о ребрах графа:
-
Определение и роль: Ребра графа представляют собой связи между вершинами. В неориентированном графе ребро соединяет две вершины, в то время как в ориентированном графе оно имеет направление, указывающее, от какой вершины к какой оно ведет. Ребра играют ключевую роль в определении структуры графа и его свойств, таких как связность и кратчайшие пути.
-
Типы ребер: В графах можно выделить различные типы ребер. Например, в ориентированных графах могут быть «первичные» и «вторичные» ребра, в зависимости от их роли в определении структуры графа. В неориентированных графах ребра могут быть «мостами» (если их удаление увеличивает количество компонент связности) или «петлями» (если они соединяют вершину саму с собой).
-
Применение в реальной жизни: Ребра графа находят широкое применение в различных областях, таких как компьютерные сети, социальные сети, транспортные системы и биоинформатика. Например, в социальных сетях вершины могут представлять пользователей, а ребра — их взаимодействия, что позволяет анализировать динамику общения и выявлять сообщества.
Эти факты подчеркивают важность ребер в графах и их применение в различных сферах.

Пошаговый анализ и практические примеры работы с ребрами графа
Рассмотрим наглядный пример создания и анализа графа с разнообразными типами ребер, используя в качестве иллюстрации транспортную сеть города. Первым шагом будет определение вершин графа — в нашем случае это ключевые транспортные узлы, такие как перекрестки, станции метро и автобусные остановки. На следующем этапе необходимо установить связи между этими узлами, то есть определить ребра графа. Для этого следует выполнить следующие действия:
- Сбор информации о действующих маршрутах и их характеристиках
- Классификация дорог по типам (односторонние и двусторонние)
- Определение временных параметров для каждого участка дороги
- Учет ограничений по пропускной способности
| Этап | Действие | Необходимые данные | Инструменты |
|---|---|---|---|
| 1 | Идентификация вершин | Картографические данные | GIS-системы |
| 2 | Определение связей | Транспортные схемы | Графовые базы данных |
| 3 | Установка весов | Статистика движения | Инструменты анализа данных |
| 4 | Настройка ограничений | Правила дорожного движения | Программное обеспечение для моделирования трафика |
Артём Викторович Озеров делится своим опытом: «При разработке проекта по оптимизации маршрутного такси мы столкнулись с необходимостью одновременно учитывать несколько типов ребер: постоянные связи между остановками, временные ограничения на движение и изменяющуюся загруженность дорог в разное время суток.» Это потребовало создания многослойной модели графа с различными типами ребер.
Ключевым моментом в работе с ребрами графа является корректная интерпретация результатов анализа. Например, при поиске оптимального маршрута важно учитывать не только кратчайший путь, но и другие характеристики ребер: возможные пробки, светофоры и ограничения скорости. Евгений Игоревич Жуков подчеркивает: «В реальных системах часто возникает необходимость динамического пересчета характеристик ребер в реальном времени, что требует применения специализированных алгоритмов и мощных вычислительных ресурсов.»
Современные подходы показывают, что наиболее эффективным является комбинированное использование различных типов ребер. Например, в навигационных системах одни ребра могут представлять постоянные связи между точками маршрута (неориентированные), другие — временные ограничения (ориентированные), а третьи — динамически изменяющуюся загруженность (взвешенные динамические). Такой комплексный подход позволяет создавать более точные и адаптивные модели транспортных потоков.
Распространенные ошибки и способы их избежания
При анализе графов специалисты часто сталкиваются с распространенными ошибками, которые могут значительно повлиять на результаты и качество принимаемых решений. Одной из наиболее частых проблем является неверное определение типа ребра для конкретной задачи. Например, применение неориентированных ребер в ситуациях, где необходимо учитывать направление движения, может привести к ошибочным выводам в области транспортной логистики. Исследования 2024 года показывают, что около 40% ошибок в сетевом анализе связаны именно с неправильным выбором типа ребер.
Еще одной серьезной проблемой является игнорирование динамических характеристик ребер. Многие специалисты продолжают использовать статические модели в тех случаях, когда необходимо учитывать временные изменения. «Я часто наблюдаю, как молодые специалисты создают модели с фиксированными весами ребер для анализа транспортных потоков, не принимая во внимание суточные колебания интенсивности движения,» — отмечает Евгений Игоревич Жуков. Это может привести к значительным ошибкам в расчетах и неэффективным решениям.
Таблица распространенных ошибок и их последствий:
| Ошибка | Пример | Последствия | Способ предотвращения |
| Неверный выбор типа ребра | Применение неориентированных ребер для одностороннего движения | Некорректные маршруты | Тщательный анализ задачи |
| Игнорирование динамики | Фиксированные веса для транспортных потоков | Неадекватные прогнозы | Внедрение временных рядов |
| Недостаточная детализация | Объединение нескольких связей в одно ребро | Утрата важной информации | Подробное моделирование |
| Неверная интерпретация весов | Использование расстояния вместо времени в пути | Неоптимальные маршруты | Четкое определение метрик |
Артём Викторович Озеров подчеркивает еще одну распространенную ошибку: «Многие специалисты забывают о необходимости нормализации весов ребер при работе с разнородными данными, что может привести к искаженным результатам в алгоритмах оптимизации.» Для предотвращения данной проблемы рекомендуется применять стандартизированные методы преобразования данных и проводить предварительный анализ масштабов различных параметров.
Современные исследования подтверждают, что внедрение автоматизированных систем для проверки корректности определения ребер может снизить количество ошибок на 60-70%. Это особенно важно в критически важных системах, таких как управление воздушным движением или медицинская диагностика. Поэтому настоятельно рекомендуется использовать специализированное программное обеспечение для верификации моделей графов перед их практическим применением.
Вопросы и ответы по теме ребер графа
Рассмотрим наиболее распространенные вопросы, возникающие при работе с ребрами графа, и их решения:
-
Как понять, нужно ли использовать взвешенные ребра?
Ответ: Если в вашей задаче имеются количественные параметры, отражающие связи между объектами (например, расстояние, время или стоимость), то применение взвешенных ребер становится необходимым. К примеру, при планировании логистических маршрутов вес ребер может обозначать время доставки или затраты на транспортировку. -
Что делать, если данные о свойствах ребер противоречат друг другу?
Решение: В таких случаях стоит применять методы статистической обработки для выявления наиболее вероятных значений. Можно использовать скользящее среднее или медианную фильтрацию для анализа временных рядов. В более сложных ситуациях рекомендуется создавать несколько параллельных моделей с различными наборами параметров. -
Как учесть несколько характеристик ребра одновременно?
Ответ: Эффективным подходом будет использование многомерных весов или создание нескольких слоев графа. Например, один слой может отображать расстояние, другой — время в пути, а третий — стоимость. Современные графовые базы данных способны работать с такими сложными структурами. -
Как справляться с изменяющимися свойствами ребер?
Решение: Внедрение динамических моделей с использованием временных рядов и прогнозных алгоритмов. Важно регулярно обновлять данные и пересчитывать характеристики ребер. Автоматизированные системы мониторинга помогают поддерживать актуальность информации. -
Что делать, если обнаружены кратные ребра?
Ответ: Кратные ребра требуют особого подхода в зависимости от конкретной задачи. Их можно либо объединить в одно ребро с усредненными характеристиками, либо оставить как отдельные связи, если каждая из них имеет самостоятельное значение. Выбор метода зависит от специфики решаемой задачи.
Евгений Игоревич Жуков делится своим опытом: «При работе с финансовыми потоками мы часто сталкиваемся с необходимостью одновременно учитывать несколько характеристик ребер: объем транзакций, их частоту и уровень риска. Мы применяем многомерные веса и специальные алгоритмы нормализации для корректной обработки такой информации.»
Заключение и рекомендации
В заключение следует подчеркнуть, что осознание природы и особенностей ребер графа является важнейшим аспектом для успешного решения множества практических задач в самых разных сферах. Точность моделей и эффективность принимаемых решений во многом зависят от правильного определения типов ребер и их характеристик. Необходимо учитывать, что выбор подходящих типов ребер должен основываться на тщательном анализе специфики задачи и доступных данных.
Для достижения наилучших результатов рекомендуется:
— Проводить тщательный анализ требований задачи перед созданием графовой модели
— Использовать современные инструменты для работы с различными типами ребер
— Регулярно обновлять характеристики ребер в динамических системах
— Применять методы верификации моделей перед их практическим применением
При работе со сложными графовыми структурами, особенно в критически важных системах, целесообразно обратиться за более подробной консультацией к квалифицированным специалистам. Они помогут правильно определить типы ребер, настроить их характеристики и выбрать оптимальные методы анализа для конкретной задачи.
Связь ребер графа с другими структурами данных
Ребра графа играют ключевую роль в представлении и анализе различных структур данных. Они не только соединяют вершины, но и определяют свойства графа, такие как связность, направленность и вес. Понимание связи ребер графа с другими структурами данных позволяет более эффективно использовать графы в различных приложениях, включая компьютерные сети, социальные сети, маршрутизацию и многие другие области.
Одной из наиболее распространенных структур данных, с которой связаны ребра графа, является матрица смежности. В этой структуре данные о ребрах хранятся в виде двумерного массива, где строки и столбцы соответствуют вершинам графа. Если существует ребро между двумя вершинами, то соответствующий элемент матрицы будет иметь значение, отличное от нуля (в случае взвешенного графа — это вес ребра). Эта структура позволяет быстро проверять наличие ребра между двумя вершинами, но может занимать много памяти, особенно для разреженных графов.
Другой распространенной структурой является список смежности, который представляет граф в виде массива списков. Каждый элемент массива соответствует вершине графа и содержит список всех вершин, с которыми она соединена ребрами. Этот подход более эффективен для разреженных графов, так как требует меньше памяти и позволяет быстро перебирать соседние вершины. Связь между ребрами и списком смежности позволяет легко добавлять и удалять ребра, что делает эту структуру более гибкой для динамических графов.
Ребра графа также могут быть связаны с другими структурами данных, такими как деревья и сети. Например, в деревьях каждое ребро соединяет родительскую вершину с дочерней, что позволяет эффективно организовывать иерархические данные. В сетях, таких как транспортные или коммуникационные, ребра могут представлять собой маршруты или каналы передачи данных, где важно учитывать не только наличие ребра, но и его характеристики, такие как пропускная способность и задержка.
Кроме того, в алгоритмах, работающих с графами, ребра играют важную роль в определении путей и циклов. Алгоритмы поиска, такие как поиск в глубину и поиск в ширину, используют ребра для навигации по графу, а алгоритмы нахождения кратчайшего пути, такие как алгоритм Дейкстры и алгоритм Флойда-Уоршелла, опираются на веса ребер для вычисления оптимальных маршрутов.
Таким образом, ребра графа являются неотъемлемой частью множества структур данных и алгоритмов, что делает их важным объектом изучения в области информатики и смежных дисциплин. Понимание их связи с другими структурами данных позволяет разработчикам и исследователям более эффективно решать задачи, связанные с анализом и обработкой графов.
Вопрос-ответ
Что такое ребра в графах?
Ребро (или звено) сети (или графа) — это одно из соединений между узлами (или вершинами) сети. Ребра могут быть направленными, то есть направленными от одного узла к другому, как показано стрелками на первом рисунке ниже.
Что называют рёбрами графа?
Соединения между узлами графа называются ребрами. Если узлы графа не нумерованы, то ребра являются неориентированными. У графа с нумерованными узлами ребра ориентированы. Ребрам могут быть присвоены определенные веса или метки.
Как понять, сколько рёбер у графа?
Количество рёбер графа равно половине суммы степеней его вершин.
Что такое вершина и ребро графа?
Ребро — это линия пересечения двух граней фигуры (куба, прямоугольной призмы и др.). Вершина — это точка пересечения трёх рёбер фигуры.
Советы
СОВЕТ №1
Изучите основные понятия теории графов, такие как вершины, рёбра и типы графов. Это поможет вам лучше понять, как рёбра графа взаимодействуют с вершинами и какую роль они играют в структуре графа.
СОВЕТ №2
Практикуйтесь на примерах. Попробуйте самостоятельно построить графы с различными рёбрами и вершинами, чтобы увидеть, как они влияют на свойства графа, такие как связность и кратчайшие пути.
СОВЕТ №3
Изучите алгоритмы, связанные с рёбрами графа, такие как алгоритм Дейкстры или алгоритм Краскала. Понимание этих алгоритмов поможет вам применять теорию на практике и решать реальные задачи.
СОВЕТ №4
Обратите внимание на приложения графов в различных областях, таких как компьютерные сети, социальные сети и биоинформатика. Это поможет вам увидеть, как теория графов используется в реальной жизни и какие задачи можно решать с её помощью.