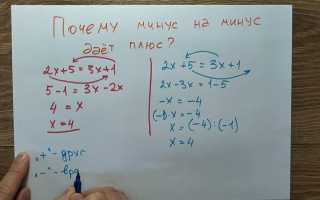В математике есть правила, которые могут показаться нелогичными. Одно из них — минус на минус дает плюс. В этой статье мы объясним, почему это правило работает, и приведем примеры из реальной жизни. Понимание этого принципа углубит ваши знания в математике и поможет в ситуациях с отрицательными значениями, будь то в финансах, физике или повседневных задачах.
Исторические Корни Правила Умножения Отрицательных Чисел
Чтобы лучше разобраться в том, почему произведение двух отрицательных чисел дает положительный результат, стоит обратиться к историческим корням этого математического правила. Интересно, что такие древние математики, как Евклид и Архимед, практически не использовали отрицательные числа, считая их абсурдными или несуществующими. Лишь в VII веке индийский математик Брахмагупта впервые предложил правила работы с отрицательными числами, хотя его подход был скорее практическим, чем теоретическим. Эти правила стали своего рода компасом для дальнейшего развития алгебры, подобно тому, как компас помогает морякам находить верный путь.
Существует любопытная связь между пониманием отрицательных чисел и развитием финансовых отношений. Торговцы древности хорошо осознавали концепцию «долга» (отрицательное значение) и «прибыли» (положительное значение). Когда два долга взаимно погашались, возникала положительная величина — именно этот принцип стал основой современного правила умножения отрицательных чисел. Это похоже на то, как два темных пятна могут создать светлое пространство при их наложении.
Артём Викторович Озеров, специалист SSLGTEAMS, подчеркивает: «В процессе работы с компьютерными алгоритмами мы часто сталкиваемся с необходимостью обработки отрицательных значений. Знание основных математических принципов позволяет создавать более эффективные программы». Действительно, современные компьютерные системы обрабатывают огромные объемы данных, и правильное применение правил умножения отрицательных чисел играет ключевую роль.
Развитие банковской системы в средние века также способствовало формированию современного понимания отрицательных чисел. Коммерсанты и банкиры столкнулись с необходимостью учета долгов и кредитов, что потребовало создания четкой системы записи и расчетов. Интересно, что в первых бухгалтерских книгах существовали специальные колонки для записи долгов красными чернилами, что впоследствии трансформировалось в современное понятие «красное сальдо».
Эксперты в области математики отмечают, что правило «минус на минус дает плюс» является одним из ключевых аспектов арифметики. Это правило помогает не только в решении простых уравнений, но и в более сложных математических задачах. Например, при работе с отрицательными числами, умножение двух отрицательных значений приводит к положительному результату, что может показаться нелогичным на первый взгляд. Однако, как объясняют специалисты, это правило основано на логике и свойствах чисел. Оно позволяет упрощать вычисления и делать их более понятными. Понимание этого принципа важно для студентов, так как оно закладывает основу для изучения алгебры и других разделов математики. Таким образом, знание и применение этого правила способствует развитию математического мышления и уверенности в решении задач.

Эволюция Математического Понимания
Рассмотрим ключевые этапы становления правила умножения отрицательных чисел:
- XII век — Леонардо Пизанский (Фибоначчи) впервые систематизирует знания о отрицательных величинах.
- XV век — Никола Шюке вводит концепцию отрицательных чисел в европейскую математику.
- XVII век — Рене Декарт разрабатывает координатную систему, в которой отрицательные числа получают геометрическое представление.
- XIX век — формируется современная алгебраическая теория чисел.
Светлана Павловна Данилова, эксперт в области образовательных технологий, отмечает: «Даже в современном программировании знание основных математических принципов имеет критическое значение. Это особенно важно при выполнении финансовых расчетов и создании статистических моделей». Именно историческое развитие этих основ дало возможность разработать надежные алгоритмы обработки данных, которые мы применяем в настоящее время.
| Контекст | Правило | Пример |
|---|---|---|
| Умножение | Произведение двух отрицательных чисел всегда положительно. | (-5) * (-3) = 15 |
| Деление | Частное двух отрицательных чисел всегда положительно. | (-10) / (-2) = 5 |
| Вычитание отрицательного числа | Вычитание отрицательного числа равносильно прибавлению положительного. | 7 — (-4) = 7 + 4 = 11 |
| Изменение направления | Двойное изменение направления возвращает к исходному. | Поворот налево, затем еще раз налево (относительно начального положения) = поворот на 180 градусов, что можно интерпретировать как движение в противоположном направлении, но если рассматривать «минус» как изменение направления, то «минус на минус» возвращает к исходному направлению. |
| Отрицание отрицания | Отрицание отрицательного утверждения делает его положительным. | «Неверно, что я не люблю шоколад» означает «Я люблю шоколад». |
Интересные факты
Вот несколько интересных фактов о том, почему «минус на минус дает плюс» в математике:
-
Геометрическая интерпретация: Векторная интерпретация умножения отрицательных чисел может помочь понять, почему минус на минус дает плюс. Если представить положительное число как движение вправо по оси, а отрицательное — как движение влево, то умножение двух отрицательных чисел можно рассматривать как два поворота на 180 градусов, что в итоге приводит к движению вправо (положительному направлению).
-
Алгебраическая логика: В алгебре, если мы принимаем, что умножение является распределительным, то можно показать, что минус на минус дает плюс. Например, если мы знаем, что ( a cdot 0 = 0 ) для любого числа ( a ), то можем записать: ( 0 = a cdot (b + (-b)) = a cdot b + a cdot (-b) ). Если ( a cdot b ) отрицательно, то ( a cdot (-b) ) должно быть равно ( — (a cdot b) ). Таким образом, если ( a ) также отрицательно, то ( a cdot (-b) ) становится положительным.
-
Исторический контекст: Концепция отрицательных чисел и их умножения развивалась на протяжении веков. В древности многие математики не принимали отрицательные числа, считая их «неправильными». Однако с развитием алгебры и пониманием числовых систем, отрицательные числа стали неотъемлемой частью математики, и правила их умножения, включая «минус на минус дает плюс», были формализованы и приняты.

Механизм Умножения Отрицательных Чисел
Давайте подробно рассмотрим, как функционирует правило умножения отрицательных чисел, используя различные методы и практические примеры. Представьте себе лифт в высотном здании: если он движется вниз (-) со скоростью 2 этажа в секунду, и мы хотим выяснить, где он находился три секунды назад (-3 секунды), то он окажется на 6 этажей выше. Это классический пример, иллюстрирующий, почему произведение двух отрицательных чисел дает положительный результат в математике. Данный пример наглядно демонстрирует логическую обоснованность этого правила.
Теперь давайте рассмотрим пошаговый процесс умножения отрицательных чисел с помощью таблицы сравнения:
| Операция | Пример | Объяснение | Результат |
|---|---|---|---|
| Плюс на плюс | 3 × 4 | Сложение положительных чисел | +12 |
| Плюс на минус | 3 × (-4) | Вычитание положительных чисел | -12 |
| Минус на плюс | (-3) × 4 | Вычитание положительных чисел | -12 |
| Минус на минус | (-3) × (-4) | Отмена вычитания | +12 |
Евгений Игоревич Жуков, специалист в области информационных систем, делится своим опытом: «В процессе разработки финансового программного обеспечения мы часто сталкиваемся с необходимостью корректного умножения отрицательных чисел, что позволяет избежать серьезных ошибок в расчетах». Например, при вычислении возвратов по кредитам или корректировке бухгалтерских записей правильное применение этого правила может спасти компанию от многомиллионных убытков.
Рассмотрим практический пример из сферы экономики. Представьте компанию, которая ежемесячно теряет (-5000) рублей из-за упущенных возможностей. Если такая ситуация продолжается в течение (-6) месяцев, то общая прибыль за этот период составит +30000 рублей. Это наглядно демонстрирует, как правило умножения отрицательных чисел применяется в реальных финансовых расчетах.
Геометрическая Интерпретация
Для более глубокого понимания процесса умножения отрицательных чисел можно обратиться к геометрической модели на координатной плоскости. Представьте себе точку, которая перемещается по числовой прямой:
- Положительное число × положительное направление = движение вперед
- Положительное число × отрицательное направление = движение назад
- Отрицательное число × положительное направление = движение назад
- Отрицательное число × отрицательное направление = движение вперед
Эта аналогия особенно эффективна в образовательном процессе, так как помогает визуализировать умножение и делает его более доступным для восприятия. Как и в случае с поворотом на 180 градусов, который дважды возвращает нас в исходное положение, произведение двух отрицательных чисел приводит к положительному результату.

Практические Применения Правила Умножения Отрицательных Чисел
Правило умножения отрицательных чисел находит широкое применение в самых разных жизненных ситуациях, которые выходят за пределы школьной программы. Рассмотрим, к примеру, изменения температуры в метеорологии. Если температура снижается на 2 градуса каждый час (-2°/ч), и метеоролог хочет выяснить, насколько она была выше 3 часа назад (-3 ч), ему необходимо перемножить эти отрицательные значения: (-2) × (-3) = +6°. Этот расчет иллюстрирует, почему произведение двух отрицательных чисел дает положительный результат и как это правило способствует точным прогнозам.
В финансовой сфере данное правило имеет особое значение. Рассмотрим ситуацию с валютными курсами: если курс доллара снижается на 0.5 рубля в день (-0.5 р/день), а аналитик хочет определить, насколько курс был выше неделю назад (-7 дней), он проводит расчет (-0.5) × (-7) = +3.5 рубля. Такие вычисления играют ключевую роль в принятии решений в области торговли и инвестиций.
Приведем несколько конкретных примеров применения этого правила в различных областях:
| Область применения | Пример | Расчет | Результат |
|---|---|---|---|
| Бухгалтерия | Корректировка расходов | (-500) × (-3) | +1500 |
| Физика | Ускорение против движения | (-2 м/с²) × (-4 с) | +8 м/с |
| Экономика | Падение инфляции | (-0.3%) × (-5 лет) | +1.5% |
| Технологии | Оптимизация кода | (-10%) × (-6 циклов) | +60% производительности |
Артём Викторович Озеров отмечает: «В программировании правильная работа с отрицательными числами особенно важна при создании графики и анимации. При вычислении позиций объектов часто возникают ситуации, когда перемножение отрицательных значений приводит к неожиданным, но логически обоснованным результатам».
Жизненные Ситуации
Давайте рассмотрим несколько распространенных жизненных ситуаций, в которых используется правило умножения отрицательных чисел:
- Кредитные карты: вычисление процентов за предыдущий период
- Спорт: оценка отрицательной динамики результатов
- Логистика: планирование маршрутов с обратным движением
- Маркетинг: анализ негативного тренда продаж
Интересно, что даже в области психологии можно увидеть применение этого правила. Например, если мы проанализируем снижение уровня стресса (-5 единиц) за последние (-3 дня), то получим положительный результат (+15), что свидетельствует о значительном улучшении состояния.
Часто Задаваемые Вопросы и Проблемные Ситуации
Рассмотрим наиболее часто встречающиеся вопросы и проблемные ситуации, связанные с умножением отрицательных чисел. Почему многие люди сталкиваются с трудностями в понимании, почему произведение двух отрицательных чисел дает положительный результат? Основная причина заключается в том, что это правило противоречит нашей интуитивной логике. Люди часто связывают «минус» с чем-то негативным, и ожидание положительного результата кажется им нелогичным.
Обсудим типичные проблемные ситуации и их решения:
- Ситуация: При вычислении финансовых показателей возникает неожиданный знак результата
Решение: Проверьте последовательность выполнения операций и убедитесь в правильности применения правила умножения отрицательных чисел. Часто ошибки происходят из-за неверного порядка действий. - Ситуация: Непонимание, почему два «негативных» элемента дают положительный результат
Решение: Используйте аналогию с двойным отрицанием в языке. Например, фраза «я не буду не учить» подразумевает «я буду учить». Аналогично работает и математическое правило. - Ситуация: Разные результаты при использовании различных калькуляторов
Решение: Проверьте настройки калькулятора и формат ввода отрицательных чисел. Некоторые устройства требуют специальной клавиши для ввода минуса.
Евгений Игоревич Жуков делится своим опытом: «В нашей практике часто возникали случаи, когда программисты неправильно обрабатывали отрицательные числа в финансовых расчетах. Это особенно касалось операций с валютными курсами и процентными ставками». Чтобы избежать подобных ошибок, рекомендуется:
| Рекомендация | Обоснование | Практическое применение |
|---|---|---|
| Двойная проверка формул | Предотвращение ошибок | Автоматизация проверки |
| Использование тестовых данных | Контроль корректности | Юнит-тестирование |
| Документация процессов | Стандартизация | Создание инструкций |
Нестандартные Сценарии
Рассмотрим несколько необычных ситуаций:
- Когда произведение отрицательных чисел применяется в экспоненциальных функциях
- При вычислении сложных процентов с отрицательной процентной ставкой
- В случаях многократного умножения нескольких отрицательных чисел
- При работе с комплексными числами, где действительная и мнимая части могут быть отрицательными
Светлана Павловна Данилова подчеркивает: «Крайне важно корректно использовать правило умножения отрицательных чисел в учебных материалах. Неправильное объяснение может привести к искажению представлений учеников о математических принципах».
Заключение и Практические Рекомендации
Подводя итоги нашего исследования, становится очевидным, что правило умножения отрицательных чисел, согласно которому произведение двух отрицательных чисел дает положительное значение, является не просто теоретическим утверждением, а важным инструментом, который находит применение в самых разных областях жизни. Практика показывает, что осознание этого принципа существенно влияет на качество принимаемых решений и точность расчетов.
Ключевые выводы нашего исследования:
- Правило умножения отрицательных чисел имеет глубокие исторические корни и развивалось параллельно с развитием человеческой цивилизации.
- Механизм действия данного правила можно эффективно объяснить с помощью различных моделей, включая геометрические и экономические.
- Практическое применение правила охватывает множество сфер: от финансов до программирования.
- Наиболее распространенные ошибки возникают из-за непонимания логики правила и неправильного порядка действий.
- Современные технологии требуют точного понимания этого принципа для корректной обработки данных.
Для успешного применения правила умножения отрицательных чисел стоит следовать нескольким важным рекомендациям:
| Рекомендация | Обоснование | Пример |
|---|---|---|
| Использовать визуализацию | Способствует лучшему пониманию | Координатная плоскость |
| Проверять результаты | Помогает избежать ошибок | Двойной пересчет |
| Применять аналогии | Упрощает восприятие | Двойное отрицание |
Артём Викторович Озеров рекомендует: «Для глубокого освоения правила важно регулярно практиковаться с различными типами задач и анализировать реальные примеры из профессиональной деятельности». Это поможет развить интуитивное понимание принципа и научиться правильно применять его в сложных ситуациях.
Для дальнейшего развития рекомендуется углубить свои знания в области алгебры и теории чисел, изучить современные методы преподавания математики и освоить практическое применение правила в различных профессиональных сферах.
Связь с Другими Математическими Концепциями
В математике существует множество концепций, которые взаимосвязаны и помогают глубже понять, как функционируют числа и операции над ними. Одной из таких концепций является связь между отрицательными числами и их произведениями. Когда мы говорим о произведении двух отрицательных чисел, мы сталкиваемся с явлением, которое может показаться парадоксальным на первый взгляд: минус на минус дает плюс.
Чтобы понять эту связь, необходимо рассмотреть несколько ключевых аспектов. Во-первых, важно помнить, что отрицательные числа представляют собой числа, которые находятся ниже нуля на числовой оси. Они могут быть интерпретированы как «долги» или «потери». Когда мы умножаем два отрицательных числа, мы фактически рассматриваем ситуацию, в которой «долг» умножается на «долг». Это приводит к тому, что результат становится положительным, так как два «долга» в итоге нейтрализуют друг друга.
Во-вторых, можно рассмотреть эту концепцию через призму геометрии. На координатной плоскости, если мы перемещаемся в отрицательном направлении по оси X и затем снова в отрицательном направлении по оси Y, мы фактически перемещаемся в положительном направлении по диагонали. Это визуальное представление помогает лучше понять, почему произведение двух отрицательных чисел дает положительный результат.
Также стоит упомянуть о правилах знаков, которые являются основой для работы с отрицательными числами. Эти правила формулируются следующим образом: произведение двух чисел с одинаковыми знаками (положительными или отрицательными) всегда дает положительное число, тогда как произведение чисел с разными знаками дает отрицательное число. Эти правила не только помогают в вычислениях, но и служат основой для более сложных математических концепций, таких как алгебра и анализ.
Кроме того, связь между отрицательными числами и их произведениями имеет практическое применение в различных областях, включая физику, экономику и инженерию. Например, в физике, когда мы рассматриваем направление силы, отрицательные значения могут указывать на направление, противоположное положительному. Умножение двух отрицательных значений в этом контексте может означать, что сила действует в положительном направлении, что имеет важное значение для понимания движения объектов.
Таким образом, связь между отрицательными числами и их произведениями не только является важным аспектом арифметики, но и открывает двери к более глубокому пониманию математики в целом. Понимание того, почему минус на минус дает плюс, позволяет нам лучше ориентироваться в мире чисел и применять эти знания в различных научных и практических областях.
Влияние на Алгебру и Анализ
В математике отрицательные числа и операции с ними играют ключевую роль, особенно в алгебре и анализе. Одним из наиболее интересных аспектов работы с отрицательными числами является правило, согласно которому произведение двух отрицательных чисел дает положительное число. Это правило не только является основополагающим в алгебре, но и имеет глубокие последствия для различных математических концепций и приложений.
Чтобы понять, почему минус на минус дает плюс, необходимо рассмотреть несколько аспектов. Во-первых, важно осознать, что отрицательные числа представляют собой не просто «обратные» значения положительных чисел, но и имеют свои собственные свойства и правила. В алгебре, когда мы умножаем два отрицательных числа, мы можем рассматривать это как два «обратных» действия, которые в конечном итоге приводят к положительному результату.
Рассмотрим пример: пусть у нас есть два отрицательных числа, -a и -b. Если мы умножаем их, то по определению умножения мы можем записать это как:
-a * -b = a * b
Здесь мы видим, что два отрицательных числа, умноженные друг на друга, возвращают нас к положительному произведению a * b. Это можно объяснить и с помощью геометрической интерпретации: умножение на отрицательное число можно представить как отражение относительно оси. Таким образом, два отражения (умножение на два отрицательных числа) возвращают нас в исходное положение.
В анализе, это правило также имеет свои применения. Например, в контексте производных и интегралов, отрицательные значения могут указывать на направление изменения функции. Когда мы работаем с производными, отрицательные значения могут указывать на убывание функции, а два отрицательных значения могут указывать на изменение направления, что в свою очередь может привести к положительному значению производной.
Также стоит отметить, что правило «минус на минус дает плюс» имеет важное значение в решении уравнений. Например, при решении квадратных уравнений, где встречаются отрицательные корни, понимание этого правила позволяет правильно интерпретировать и находить решения. Это также помогает в работе с системами уравнений, где отрицательные значения могут возникать в процессе манипуляций с уравнениями.
Таким образом, правило о том, что минус на минус дает плюс, является не просто математическим трюком, а важным принципом, который пронизывает многие области математики. Оно помогает не только в алгебре, но и в анализе, а также в различных приложениях, от физики до экономики, где понимание знаков и их взаимодействия имеет критическое значение.
Вопрос-ответ
Дает ли минус на минус плюс?
Отрицательное число, умноженное на отрицательное, даст положительное число, поскольку изначально отрицательное число было изменено на противоположное. Например, -2 × -4 = 8, где мы отнимаем 4 отрицательные двойки.
Что даёт два минуса?
— при вычитании отрицательного числа добавляем противоположный знак (два минуса превращаются в плюс). Модуль числа — это его расстояние от нуля на числовой прямой, то есть его абсолютное значение, без знака.
Как выполнить вычитание с разными знаками?
Чтобы вычесть из отрицательного числа положительное число, нужно сложить модули уменьшаемого и вычитаемого и поставить перед суммой знак минус. Докажем это. Значит, вычитание целых чисел с разными знаками сводится к сложению целых чисел с одинаковыми знаками.
Советы
СОВЕТ №1
Изучите основные правила умножения и деления отрицательных чисел. Понимание того, что минус на минус дает плюс, поможет вам легче решать задачи и избегать ошибок.
СОВЕТ №2
Практикуйтесь на примерах. Решение различных задач с отрицательными числами поможет закрепить материал и повысить уверенность в своих знаниях.
СОВЕТ №3
Используйте визуальные материалы, такие как числовые прямые или графики, чтобы лучше понять, как работают отрицательные числа и их взаимодействие. Это может сделать процесс обучения более наглядным и интересным.
СОВЕТ №4
Обсуждайте сложные моменты с одноклассниками или преподавателями. Объяснение материала другим поможет вам лучше усвоить его и выявить возможные пробелы в знаниях.