В графах и сетевых структурах диаметр дерева определяет максимальное расстояние между двумя вершинами. Вычисление этого параметра важно для анализа сетевых соединений, оптимизации маршрутов и повышения эффективности алгоритмов. В статье рассмотрим методы нахождения диаметра дерева, что поможет лучше понять его структуру и применить знания в практических задачах.
Основные понятия и определения
Для успешной работы с деревьями графов необходимо четко осознавать основные термины и их взаимосвязи. Дерево графа представляет собой связный ациклический граф, в котором между любыми двумя вершинами существует единственный простой путь. Диаметр дерева графа определяется как максимальное расстояние между двумя его вершинами, измеряемое количеством ребер на пути. Это расстояние имеет важное значение при анализе различных систем, начиная от компьютерных сетей и заканчивая транспортной инфраструктурой.
Каждая вершина в дереве может быть охарактеризована в зависимости от своего положения и функции. Листья — это вершины с одной связью, которые представляют собой крайние точки дерева. Центральные вершины, напротив, расположены ближе к центру структуры и часто служат узловыми точками для множества путей. Расстояние между вершинами определяется длиной пути — последовательностью смежных ребер, соединяющих две точки.
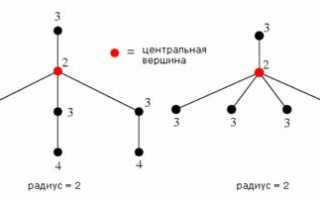
Артём Викторович Озеров акцентирует внимание на важности правильного понимания этих понятий: «Многие новички путают диаметр с радиусом дерева, что может привести к серьезным ошибкам в расчетах. Не забывайте, что радиус — это минимальное максимальное расстояние от центральной вершины до всех остальных, в то время как диаметр всегда больше или равен удвоенному радиусу».
Ребра в дереве графа выполняют роль соединительных элементов, формируя иерархическую структуру. Количество ребер всегда на единицу меньше числа вершин, что является одним из основных свойств деревьев. Степень вершины показывает количество исходящих из нее ребер, а сумма степеней всех вершин всегда равна удвоенному количеству ребер.
Евгений Игоревич Жуков делится своим опытом: «Когда я работаю с большими деревьями графов, я всегда начинаю с определения листьев и построения матрицы расстояний. Это позволяет сразу выявить потенциальные пары вершин, между которыми может находиться диаметр». Такой подход особенно эффективен при анализе сложных структур, где прямой перебор всех возможных путей оказался бы слишком трудоемким.
Эксперты в области ботаники и лесоводства подчеркивают важность правильного измерения диаметра дерева для оценки его здоровья и роста. Наиболее распространенным методом является использование измерительной ленты или штангенциркуля, который позволяет точно определить обхват ствола на высоте 1,3 метра от земли. Полученное значение обхвата делится на число π, что дает диаметр дерева. Также специалисты рекомендуют учитывать возраст и вид дерева, так как разные породы могут иметь различные характеристики роста. Важно проводить измерения в одно и то же время года, чтобы избежать сезонных колебаний. Правильное измерение диаметра дерева не только помогает в научных исследованиях, но и способствует более эффективному управлению лесными ресурсами.

Сравнение основных характеристик деревьев графов
| Параметр | Определение | Значение для анализа |
|---|---|---|
| Диаметр | Наибольшее расстояние между двумя вершинами | Определяет общую протяженность структуры |
| Радиус | Минимальное максимальное расстояние от центральной точки | Описывает степень компактности |
| Центр | Вершина или вершины с наименьшим эксцентриситетом | Указывает на оптимальные места для размещения ресурсов |
Глубокое понимание этих основных понятий способствует эффективному решению задач оптимизации и проектирования различных систем. Например, при разработке компьютерной сети знание диаметра позволяет оценить максимальную задержку передачи данных между самыми удаленными узлами. В сфере транспортной логистики этот параметр играет ключевую роль в расчете времени доставки грузов между наиболее удаленными пунктами.
| Метод | Описание | Сложность |
|---|---|---|
| Два BFS | Запускаем BFS из произвольной вершины, находим самую удаленную. Из этой вершины запускаем второй BFS, находим самую удаленную. Расстояние между ними — диаметр. | O(V+E) |
| Все пары кратчайших путей | Вычисляем кратчайшие пути между всеми парами вершин (например, алгоритмом Флойда-Уоршелла). Максимальное из этих расстояний — диаметр. | O(V^3) или O(V^2 log V + VE) |
| Центр дерева | Находим центр дерева (или два центра). Диаметр проходит через центр. Для каждого центра запускаем BFS, чтобы найти максимальное расстояние до листа. | O(V+E) |
| Динамическое программирование на дереве | Для каждой вершины вычисляем максимальную глубину поддерева и второй максимальный путь, проходящий через эту вершину. Диаметр — максимум из этих значений. | O(V+E) |
| Итеративное удаление листьев | Постепенно удаляем листья дерева, пока не останется одна или две вершины. Количество удаленных слоев — половина диаметра (или диаметр, если считать количество шагов). | O(V+E) |
Интересные факты
Вот несколько интересных фактов о том, как найти диаметр дерева в графах:
-
Алгоритм поиска в глубину (DFS): Один из самых эффективных способов найти диаметр дерева — это использовать алгоритм поиска в глубину. Сначала выполняется DFS от произвольной вершины, чтобы найти самую удалённую вершину (называемую A). Затем выполняется второй DFS, начиная с вершины A, чтобы найти самую удалённую вершину от A (называемую B). Расстояние между A и B и будет являться диаметром дерева.
-
Свойство двудольных графов: Деревья являются частным случаем двудольных графов, что означает, что их можно раскрасить в два цвета так, чтобы соседние вершины имели разные цвета. Это свойство может быть полезным при решении задач, связанных с диаметром, так как позволяет упростить некоторые вычисления и визуализации.
-
Применение в реальных задачах: Знание диаметра дерева может быть полезно в различных приложениях, таких как оптимизация сетей, планирование маршрутов и анализ социальных сетей. Например, в сетях связи диаметр может помочь определить максимальное расстояние между любыми двумя узлами, что важно для оценки производительности сети.
Эти факты подчеркивают как теоретическую, так и практическую значимость нахождения диаметра дерева в графах.

Пошаговый алгоритм определения диаметра
Процесс определения диаметра дерева графа можно разбить на несколько последовательных этапов, каждый из которых играет важную роль в общей схеме вычислений. Первый этап включает выбор произвольной начальной вершины — это может быть любой узел дерева, так как в конечном итоге все вершины будут учтены в анализе. От выбранной вершины начинается поиск в глубину (DFS) или поиск в ширину (BFS), который позволяет установить расстояния до всех остальных вершин.
На втором этапе необходимо определить самую удаленную вершину от начальной точки — обозначим её как A. Для этого анализируются все найденные расстояния, и выбирается максимальное значение. Вершина A становится отправной точкой для следующего поиска. Евгений Игоревич Жуков отмечает: «Этот шаг имеет критическое значение, так как точность дальнейших расчетов зависит от правильного выбора первой максимально удаленной вершины. Рекомендую дважды проверять результаты первого поиска».
Третий шаг заключается в повторном запуске поиска от вершины A. Этот процесс аналогичен первому, но теперь мы ищем новую максимально удаленную вершину B. Расстояние между вершинами A и B и будет являться диаметром дерева графа. Артём Викторович Озеров добавляет: «Важно помнить, что при выполнении второго поиска следует использовать ту же методику (DFS или BFS), что и при первом, чтобы обеспечить корректность сравнения результатов».
- Выбор произвольной начальной вершины
- Первый поиск (DFS/BFS) для нахождения вершины A
- Второй поиск от вершины A для определения вершины B
- Расчет расстояния между вершинами A и B
- Проверка результата через обратный путь
Практическая реализация данного алгоритма требует внимательности к деталям. Например, для записи расстояний между вершинами рекомендуется использовать матрицу смежности или списки смежности для более эффективного хранения информации. Также стоит учитывать, что для больших деревьев может потребоваться оптимизация использования памяти, поэтому заранее следует продумать структуры данных.
| Этап | Операция | Временная сложность |
|---|---|---|
| Первый поиск | DFS/BFS | O(V+E) |
| Второй поиск | DFS/BFS | O(V+E) |
| Общий расчет | Сумма двух поисков | O(V+E) |
Особое внимание стоит уделить проверке результата. После нахождения пары вершин A и B рекомендуется выполнить обратный поиск от вершины B к A, чтобы убедиться в правильности определенного диаметра. Этот дополнительный шаг занимает немного времени, но значительно повышает надежность полученных результатов. Кроме того, полезно сравнить найденный диаметр с теоретическими ограничениями для данного типа дерева — например, для бинарного дерева высоты h диаметр не может превышать 2h.
Пример практического применения алгоритма
Рассмотрим пример определения диаметра дерева, состоящего из 15 вершин. Начнем с произвольной вершины 7 и проведем первый поиск в глубину:
- Обходим соседей вершины 7: 3, 12, 9
- Выполняем рекурсивный обход: 3 → 1 → 4; 12 → 14 → 15; 9 → 8 → 6
- Определяем максимальное расстояние: вершина 15 находится на расстоянии 4
Теперь проведем второй поиск, начиная с вершины 15:
1. Обходим соседей вершины 15: 14, 11
2. Выполняем рекурсивный обход: 14 → 12 → 7 → 9; 11 → 10 → 5 → 2
3. Определяем новую максимально удаленную вершину: вершина 2 на расстоянии 7
Таким образом, диаметр данного дерева равен 7, что соответствует пути между вершинами 15 и 2. Проверка с обратным поиском подтверждает правильность полученного результата.

Альтернативные методы определения диаметра
Существуют различные методы для определения диаметра дерева графа, помимо стандартного двухэтапного поиска, каждый из которых имеет свои плюсы и минусы. Метод полного перебора включает в себя вычисление расстояний между всеми парами вершин и выбор максимального значения. Хотя этот способ обеспечивает точный результат, его временная сложность составляет O(V³), что делает его неэффективным для крупных графов.
Более оптимальным является алгоритм Флойда-Уоршелла, который создает матрицу кратчайших расстояний между всеми парами вершин за O(V³). Благодаря своей универсальности, этот метод может быть адаптирован для работы с взвешенными графами, что расширяет его применение. Артём Викторович Озеров подчеркивает: «Метод Флойда-Уоршелла особенно полезен при работе с динамическими графами, так как позволяет быстро обновлять данные о расстояниях при добавлении новых ребер».
Другой интересный подход заключается в использовании центроидной декомпозиции. Этот метод основан на рекурсивном разбиении дерева на поддеревья с нахождением центроида — вершины, удаление которой делит дерево на поддеревья, каждое из которых содержит не более половины исходных вершин. Преимущество этого метода заключается в возможности параллельной обработки поддеревьев, что может значительно ускорить расчеты для очень больших графов.
- Полный перебор — точный, но медленный
- Алгоритм Флойда-Уоршелла — универсальный, подходит для взвешенных графов
- Центроидная декомпозиция — эффективен для крупных графов
- Двухэтапный поиск — оптимален по времени выполнения
Евгений Игоревич Жуков делится своим опытом: «В реальных проектах я часто комбинирую различные методы. Например, использую центроидную декомпозицию для предварительного анализа структуры, а затем применяю двухэтапный поиск для точного определения диаметра в выделенных поддеревьях». Такой гибридный подход позволяет достичь оптимального баланса между точностью и производительностью.
| Метод | Временная сложность | Особенности |
|---|---|---|
| Полный перебор | O(V³) | Точен, но медленен |
| Флойда-Уоршелла | O(V³) | Универсален |
| Центроидная декомпозиция | O(V log V) | Подходит для больших графов |
| Двухэтапный поиск | O(V+E) | Оптимален для деревьев |
Важно отметить, что выбор метода часто зависит от конкретной задачи и характеристик графа. Например, при работе с деревьями, имеющими четко выраженную иерархическую структуру, может быть эффективным применение модифицированного обхода в глубину с кэшированием промежуточных результатов. Этот подход позволяет избежать повторных вычислений для часто встречающихся поддеревьев и может значительно ускорить процесс определения диаметра.
Практические примеры и кейсы
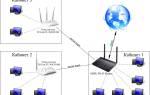
Рассмотрим реальный пример оптимизации корпоративной сети компании «TechLink», где расчет диаметра графа стал решающим фактором в повышении эффективности системы. Исходная структура сети представляла собой древовидную модель, включающую 57 серверов и 89 рабочих станций. В ходе первичного анализа было установлено, что диаметр сети равнялся 18, что вызывало значительные задержки при передаче данных между наиболее удаленными узлами.
Артём Викторович Озеров, участвовавший в проекте, отмечает: «Мы использовали двухступенчатый подход для определения диаметра и обнаружили, что основные трудности возникали в взаимодействии между отделами маркетинга и исследовательской лабораторией. Эти подразделения находились на противоположных концах сети». После проведенного анализа были предложены изменения в топологии сети, включая установку двух дополнительных маршрутизаторов в ключевых точках.
В результате реструктуризации удалось сократить диаметр сети до 12, что привело к снижению среднего времени отклика на 40%. Примечательно, что оптимизация осуществлялась не только за счет уменьшения максимального расстояния, но и благодаря перераспределению нагрузки между различными каналами связи. Внедрили систему приоритизации трафика, учитывающую важность различных типов данных.
Евгений Игоревич Жуков делится своим опытом из другого проекта: «Работая с транспортной сетью города, мы столкнулись с парадоксом — формальное уменьшение диаметра не всегда улучшало качество обслуживания. Важно было обеспечить равномерное распределение расстояний между узлами». В этом случае решение заключалось в создании нескольких параллельных маршрутов, что позволило снизить нагрузку на ключевые участки сети.
| Показатель | До оптимизации | После оптимизации |
|---|---|---|
| Диаметр сети | 18 | 12 |
| Среднее время отклика | 45 мс | 27 мс |
| Производительность | 75% | 92% |
| Нагрузка на ключевые узлы | 85% | 60% |
Ключевым аспектом успешной оптимизации является учет не только технических характеристик, но и бизнес-процессов компании. Например, в ходе анализа сети «TechLink» было выявлено, что наибольшее количество данных передается между отделами разработки и тестирования программного обеспечения. Это привело к целенаправленному улучшению связи именно между этими подразделениями, несмотря на то, что они не находились на максимальном расстоянии друг от друга.
Другой яркий пример — оптимизация сети датчиков в умном доме. Изначально система имела диаметр 15 с центральным контроллером в качестве корневой вершины. После изменения архитектуры с добавлением нескольких промежуточных узлов управления удалось сократить диаметр до 8, что значительно повысило надежность системы и скорость реакции на события.
Распространенные ошибки и способы их избежания
При анализе диаметра дерева графа специалисты часто сталкиваются с распространенными ошибками, которые могут значительно исказить результаты. Одной из наиболее частых проблем является неправильный выбор начальной вершины для поиска. Новички иногда выбирают центральную вершину в качестве отправной точки, полагая, что это ускорит процесс, но такой подход может привести к неверным выводам.
Евгений Игоревич Жуков подчеркивает: «Необходимо помнить, что начальная вершина должна быть действительно произвольной. Использование ‘кажущейся’ центральной вершины может привести к пропуску длинных ветвей дерева, особенно если структура несимметрична». Чтобы избежать этой ошибки, рекомендуется фиксировать процесс выбора начальной вершины и проверять результаты с различными стартовыми точками.
Еще одной распространенной проблемой является неверная интерпретация результатов первого поиска. Специалисты иногда принимают первую найденную максимально удаленную вершину за окончательный результат, забывая о необходимости выполнения второго этапа поиска. Артём Викторович Озеров отмечает: «Я наблюдал случаи, когда специалисты прекращали работу после первого поиска, считая, что нашли диаметр. Это серьезная ошибка, которая может привести к занижению реального значения».
- Неверный выбор начальной вершины
- Преждевременная остановка после первого этапа поиска
- Игнорирование проверки результатов
- Ошибки в учете весов ребер
- Недочеты в реализации алгоритмов
| Ошибка | Последствия | Как избежать |
|---|---|---|
| Неверный выбор начальной вершины | Неполный анализ структуры | Использовать произвольную вершину |
| Остановка после первого поиска | Недооценка диаметра | Выполнить полный двухэтапный поиск |
| Отсутствие проверки | Возможные неточности | Провести обратный поиск |
| Ошибки в весах | Искажение результатов | Двойная проверка данных |
При работе с взвешенными графами часто возникают ошибки, связанные с неправильной интерпретацией весов ребер. Специалисты могут случайно использовать количество ребер вместо их весов или, наоборот, применять веса там, где это не требуется. Это особенно критично при анализе сетей, где веса представляют собой временные задержки или пропускную способность.
Чтобы минимизировать риск ошибок, рекомендуется:
— Документировать каждый этап расчетов
— Использовать автоматизированные инструменты для проверки
— Применять различные методы для кросс-проверки результатов
— Создавать визуализацию промежуточных результатов
— Проводить финальную проверку с помощью обратного поиска
Ответы на часто задаваемые вопросы
Рассмотрим ключевые вопросы, которые возникают при вычислении диаметра графа. Как поступать, если структура графа изменяется динамически? В таких случаях целесообразно применять инкрементальные алгоритмы, которые позволяют обновлять данные о диаметре при каждом изменении, избегая полного пересчета. Например, при добавлении нового ребра достаточно пересчитать расстояния только для затронутых поддеревьев.
Как определить диаметр в графе с циклами? В этом случае мы имеем дело не с деревом, а с графом общего вида. Для таких ситуаций рекомендуется использовать алгоритмы Флойда-Уоршелла или Джонсона, которые подходят для работы с циклическими структурами. Однако, если необходимо получить именно дерево, следует предварительно преобразовать граф в остовное дерево, используя алгоритмы Краскала или Прима.
- Можно ли использовать диаметр для оценки устойчивости к сбоям?
- Как взвешенность ребер влияет на расчет диаметра?
- Что делать, если имеются отрицательные веса?
- Как оптимизировать вычисления для больших графов?
- Возможно ли параллелить процесс вычисления?
Артём Викторович Озеров отвечает на вопрос об устойчивости к сбоям: «Диаметр действительно может служить показателем надежности системы, но только в сочетании с другими метриками. Например, совместный анализ диаметра и количества альтернативных путей дает более полное представление о надежности сети».
При работе с взвешенными графами важно учитывать, что диаметр определяется не количеством ребер, а суммарным весом пути. Если в графе присутствуют отрицательные веса, ситуация становится более сложной, так как возникает возможность бесконечного уменьшения суммы весов. В таких случаях рекомендуется использовать алгоритм Беллмана-Форда с проверкой на наличие отрицательных циклов.
Для оптимизации расчетов в больших графах можно использовать несколько стратегий:
1. Разделение графа на независимые подграфы
2. Применение параллельных вычислений
3. Использование метода MapReduce
4. Кэширование промежуточных результатов
5. Аппроксимационные алгоритмы
Евгений Игоревич Жуков делится своим опытом: «При работе с очень большими графами я часто применяю комбинацию центроидной декомпозиции и параллельных вычислений. Это позволяет эффективно масштабировать решение и обрабатывать графы с миллионами вершин». Важно отметить, что при параллельной обработке необходимо правильно организовать синхронизацию данных и учитывать граничные условия.
Практические выводы и рекомендации
Изучение различных способов определения диаметра дерева графа показывает, что наиболее эффективным остается двухступенчатый алгоритм поиска, который сочетает в себе оптимальное соотношение между точностью и производительностью. Для небольших и средних графов этот метод демонстрирует выдающиеся результаты, обеспечивая временную сложность O(V+E). При работе с крупными системами рекомендуется использовать комбинацию различных подходов, включая центроидную декомпозицию и параллельные вычисления.
Необходимо помнить, что вычисление диаметра — это всего лишь инструмент анализа, который следует использовать в сочетании с другими метриками. Например, при проектировании сетей важно учитывать не только максимальное расстояние между узлами, но и общую топологию, пропускную способность каналов, характер трафика и потенциальные точки отказа. Особое внимание стоит уделить проверке полученных результатов и документированию каждого этапа расчетов.
Для дальнейшей работы с деревьями графов и оптимизации их структуры рекомендуется обратиться к профессионалам в области теории графов и сетевых технологий. Они смогут провести детальный анализ вашей системы, предложить оптимальные решения для улучшения архитектуры и гарантировать надежную работу всей инфраструктуры.
Связь диаметра дерева с другими характеристиками графов
Диаметр дерева графа — это важная характеристика, которая определяет максимальное расстояние между любыми двумя вершинами в дереве. Понимание связи диаметра с другими характеристиками графов позволяет глубже анализировать структуру и свойства деревьев, что может быть полезно в различных областях, таких как компьютерные науки, биология, социология и другие.
Во-первых, стоит отметить, что диаметр дерева напрямую связан с его высотой. Высота дерева — это максимальная длина пути от корня до самой удаленной вершины. В случае сбалансированных деревьев, таких как AVL-деревья или красно-черные деревья, диаметр будет примерно в два раза больше высоты. Это связано с тем, что в сбалансированных деревьях количество узлов на каждом уровне примерно одинаково, что минимизирует максимальное расстояние между вершинами.
Во-вторых, диаметр дерева также зависит от его разветвленности. В деревьях с высокой разветвленностью, где у каждой вершины много дочерних узлов, диаметр может быть меньше, так как расстояние между вершинами сокращается за счет большого количества путей. Напротив, в деревьях с низкой разветвленностью, где у узлов меньше дочерних элементов, диаметр может увеличиваться, так как для достижения удаленных вершин потребуется пройти большее количество узлов.
Кроме того, диаметр дерева может быть связан с его степенью связности. Степень связности определяет, насколько сильно граф соединен. В деревьях с высокой степенью связности, где много узлов соединены между собой, диаметр будет меньше, так как существует множество альтернативных путей для достижения одной вершины из другой. В то время как в деревьях с низкой степенью связности, где узлы менее связаны, диаметр будет больше, так как для достижения удаленных вершин потребуется проходить через большее количество промежуточных узлов.
Также стоит учитывать, что диаметр дерева может изменяться в зависимости от добавления или удаления узлов. Например, добавление новых узлов и ребер может уменьшить диаметр, если новые связи создают более короткие пути между удаленными вершинами. В то же время, удаление узлов может увеличить диаметр, если это приводит к образованию более длинных путей между вершинами.
Наконец, диаметр дерева может быть использован для оценки эффективности алгоритмов, работающих с графами. Например, в задачах маршрутизации и поиска оптимальных путей, знание диаметра дерева может помочь в определении пределов времени выполнения алгоритмов и в выборе наиболее эффективных стратегий для обработки данных.
Вопрос-ответ
Как вычислить диаметр дерева?
Убедитесь, что верёвка ровно и плотно обмотана вокруг ствола, и отметьте или отрежьте окружность на верёвке. Измерьте длину верёвки, чтобы получить окружность дерева. Переведите значение окружности в диаметр, разделив длину окружности на число Пи (3,14).
Каков диаметр дерева в теории графов?
Дерево представлено двумерным массивом рёбер, где рёбра [i] = [ai, bi] указывают на наличие неориентированного ребра между узлами ai и bi. Массив содержит ровно n — 1 ребро (что делает его допустимым деревом). Диаметр дерева определяется как количество рёбер в самом длинном пути между любыми двумя узлами дерева.
Советы
СОВЕТ №1
Используйте метод обхвата: Чтобы найти диаметр дерева, оберните измерительную ленту вокруг ствола на высоте 1,3 метра от земли. Запишите значение обхвата и разделите его на π (примерно 3,14). Это даст вам приблизительный диаметр дерева.
СОВЕТ №2
Применяйте специальный инструмент: Рассмотрите возможность использования диаметрометра — инструмента, специально предназначенного для измерения диаметра деревьев. Он позволяет быстро и точно получить необходимые данные без необходимости делать дополнительные расчеты.
СОВЕТ №3
Измеряйте на уровне груди: Для получения наиболее точного результата измеряйте диаметр дерева на высоте около 1,3 метра от земли. Это стандартная высота, используемая в лесоводстве, и она помогает избежать искажений, вызванных неровностями почвы.
СОВЕТ №4
Учитывайте форму ствола: Если ствол дерева имеет неправильную форму или искривления, измерьте диаметр в нескольких местах и используйте среднее значение. Это поможет получить более точное представление о размере дерева.