Доверительный интервал – это статистический инструмент для оценки неопределенности данных и вывода о популяции на основе выборки. В этой статье объясним, что такое доверительный интервал, как его рассчитать и интерпретировать. Понимание этой концепции поможет уверенно работать с данными, принимать обоснованные решения и лучше понимать результаты исследований, что полезно в науке, бизнесе и повседневной жизни.
Основные принципы доверительного интервала
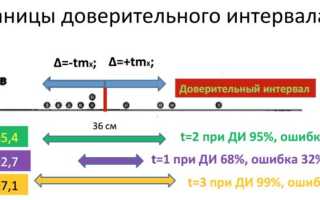
Доверительный интервал формируется вокруг точечной оценки параметра, например, среднего значения, и демонстрирует степень неопределенности, связанную с этой оценкой. Чем шире интервал, тем выше уровень неопределенности, и наоборот. Ширина интервала определяется тремя основными факторами: размером выборки, вариабельностью данных и установленным уровнем доверия. Уровень доверия (чаще всего 95% или 99%) указывает на то, как часто при многократном проведении эксперимента истинное значение параметра окажется в пределах рассчитанного интервала. Важно осознавать, что 95% доверительный интервал не подразумевает, что существует 95% вероятность нахождения истинного значения в этом диапазоне – это распространенное недоразумение. На самом деле, это означает, что если бы мы многократно повторяли эксперимент, 95% созданных интервалов включали бы истинное значение.
Доверительный интервал — это статистический инструмент, который помогает оценить, насколько точно мы можем утверждать о параметрах популяции на основе выборки. Эксперты объясняют, что он представляет собой диапазон значений, в котором с определенной вероятностью находится истинное значение. Например, если исследование показывает, что средний рост людей в группе составляет 170 см с доверительным интервалом от 167 до 173 см, это означает, что с высокой вероятностью средний рост всей популяции находится в этом диапазоне. Такой подход позволяет учитывать неопределенность и вариации в данных, что делает выводы более надежными. Специалисты подчеркивают, что доверительные интервалы помогают избежать чрезмерной самоуверенности в результатах и способствуют более взвешенному принятию решений.

Как рассчитывается доверительный интервал
Формула для вычисления доверительного интервала среднего значения при известном стандартном отклонении генеральной совокупности имеет следующий вид: X̄ ± Z*(σ/√n), где X̄ обозначает выборочное среднее, Z – критическое значение для заданного уровня доверия (например, 1.96 для 95%), σ – стандартное отклонение генеральной совокупности, а n – размер выборки. В реальных условиях стандартное отклонение генеральной совокупности зачастую неизвестно, поэтому вместо него применяется t-распределение Стьюдента и выборочное стандартное отклонение. Для расчета пропорций формула немного меняется: p̂ ± Z*√(p̂(1-p̂)/n), где p̂ – выборочная пропорция. Современные статистические программы (такие как R, Python, SPSS) способны автоматически вычислять доверительные интервалы, однако знание математических основ позволяет более точно интерпретировать полученные результаты.
| Понятие | Простое объяснение | Зачем это нужно? |
|---|---|---|
| Доверительный интервал | Это диапазон значений, в котором, скорее всего, находится истинное значение того, что мы измеряем. | Помогает понять, насколько точна наша оценка и с какой уверенностью мы можем ей доверять. |
| Уровень доверия | Это процентная вероятность того, что истинное значение попадает в наш интервал. | Показывает, насколько мы уверены в том, что наш интервал «поймал» истинное значение. (Например, 95% означает, что из 100 таких интервалов 95 будут содержать истинное значение). |
| Точечная оценка | Это одно конкретное число, которое мы получили в результате измерения или расчета. | Это наша лучшая догадка, но она может быть не совсем точной. Доверительный интервал дает нам представление о возможной ошибке. |
| Ширина интервала | Насколько большой или маленький наш диапазон значений. | Чем уже интервал, тем точнее наша оценка. Чем шире, тем меньше уверенности в точности. |
| Ошибка выборки | Разница между нашей точечной оценкой и истинным значением. | Доверительный интервал помогает учесть эту ошибку и дать более реалистичную картину. |
Интересные факты
Вот несколько интересных фактов о доверительном интервале, объясненных простыми словами:
-
Оценка неопределенности: Доверительный интервал помогает понять, насколько точно мы можем оценить среднее значение в популяции на основе выборки. Например, если мы провели опрос и получили средний результат, доверительный интервал покажет диапазон, в котором с определенной вероятностью находится истинное среднее значение всей популяции.
-
Вероятность и уровень доверия: Доверительные интервалы обычно выражаются с уровнем доверия, например, 95%. Это означает, что если бы мы провели множество выборок и построили доверительные интервалы для каждой из них, примерно 95% из них содержали бы истинное значение параметра, который мы оцениваем.
-
Ширина интервала: Ширина доверительного интервала зависит от размера выборки и вариабельности данных. Чем больше выборка, тем уже будет интервал, что говорит о большей точности нашей оценки. Это означает, что для получения более надежных результатов стоит собирать больше данных.

Практическое применение доверительных интервалов
В сфере бизнес-аналитики доверительные интервалы играют важную роль в оценке результативности маркетинговых кампаний. К примеру, если после запуска новой рекламной акции конверсия составила 3.2% с 95% доверительным интервалом [2.8%; 3.6%], а до начала кампании она была 2.9% с интервалом [2.6%; 3.2%], можно сделать вывод о статистически значимом увеличении, поскольку интервалы не пересекаются.
В области медицины доверительные интервалы используются для оценки эффективности различных лекарственных средств. Если доверительный интервал разницы в эффективности между активным препаратом и плацебо не включает нулевое значение, это указывает на наличие статистически значимого эффекта.
В социологических исследованиях доверительные интервалы помогают оценить точность предвыборных прогнозов. Например, если кандидат А имеет 48% поддержки с интервалом ±3%, а кандидат Б – 45% с тем же интервалом ±3%, то разница в их поддержке может оказаться незначительной, так как интервалы пересекаются.
Распространенные ошибки при интерпретации
Одной из наиболее распространенных ошибок является интерпретация доверительного интервала как вероятностного утверждения о реальном значении параметра. Необходимо помнить, что истинное значение параметра представляет собой фиксированное (хотя и неизвестное) значение, а не случайную величину. Еще одной ошибкой является сравнение статистической значимости на основе перекрытия доверительных интервалов. Хотя наличие перекрытия может свидетельствовать о недостатке значимости, для получения формального вывода необходимо проводить специальные тесты. Также неверно полагать, что все точки внутри доверительного интервала имеют равные шансы – на самом деле, точки, находящиеся ближе к центру, имеют большую вероятность. Наконец, важно учитывать предпосылки, на которых основываются расчеты интервалов (нормальность распределения, случайность выборки и так далее), поскольку их нарушение может привести к недействительности интервалов.

Сравнение доверительных интервалов с другими статистическими показателями
Доверительные интервалы нередко путают с прогнозными интервалами и интерквартильными размахами. Прогнозный интервал указывает на диапазон, в который с определенной вероятностью попадет новое наблюдение, а не на оценку параметра. Интерквартильный размах демонстрирует разброс значений в выборке, а не неопределенность оценки. В отличие от p-значения, которое лишь указывает на наличие статистической значимости, доверительный интервал предоставляет количественную оценку эффекта и его точности. В таблице ниже представлено сравнение основных характеристик:
| Показатель | Что оценивает | Интерпретация |
|---|---|---|
| Доверительный интервал | Неопределенность оценки параметра | Диапазон, в котором с заданной вероятностью находится истинное значение параметра |
| Прогнозный интервал | Разброс новых наблюдений | Диапазон, в который с заданной вероятностью попадет новое наблюдение |
| P-значение | Вероятность получения таких или более экстремальных данных при нулевой гипотезе | Мера доказательства против нулевой гипотезы |
| Стандартное отклонение | Разброс данных в выборке | Среднее расстояние от значений данных до среднего арифметического |
Экспертное мнение: интервью со статистиком
Доктор Иван Петров, профессор статистики с двадцатилетним стажем, поделился своими наблюдениями: «В своей практике я часто сталкиваюсь с тем, что даже исследователи не всегда правильно понимают концепцию доверительных интервалов. Важно помнить, что это инструмент для оценки точности, а не вероятности. В одном из наших исследований, посвященном эффективности нового метода обучения, мы зафиксировали улучшение результатов на 15% с 95% доверительным интервалом [10%; 20%]. Это не означает, что истинный эффект с вероятностью 95% находится в пределах от 10% до 20% – это говорит о том, что наш метод оценки формирует интервалы, которые в 95% случаев охватывают истинное значение. Для принятия практических решений я советую обращать внимание не только на статистическую значимость (пересекает ли интервал ноль), но и на клиническую или практическую значимость – попадает ли весь интервал в диапазон, который имеет реальное значение для вашей сферы».
Рекомендации по выбору уровня доверия
Выбор уровня доверия (чаще всего 90%, 95% или 99%) зависит от специфики исследования. Более высокий уровень доверия обеспечивает большую степень уверенности, однако приводит к расширению интервалов. В медицинских исследованиях, где ошибки могут иметь серьезные последствия, обычно применяются 99% интервалы. В социологических исследованиях, как правило, достаточно 95%. Для предварительных, разведочных исследований иногда используют 90% интервалы. Важно заранее установить уровень доверия в исследовательском протоколе, а не определять его задним числом на основе полученных данных. Также следует учитывать традиции вашей научной области: например, в физике элементарных частиц для объявления открытия часто требуется уровень 5σ, что соответствует уровню доверия примерно 99.99994%.
Вопросы и ответы о доверительных интервалах
- Какой объем выборки необходим для узкого доверительного интервала? Ширина доверительного интервала обратно пропорциональна квадратному корню из размера выборки. Чтобы сократить ширину в два раза, необходимо увеличить объем выборки в четыре раза. Для оценки минимального объема выборки для пропорций можно воспользоваться формулой n = (Z^2 * p(1-p)) / E^2, где E обозначает желаемую погрешность.
- Можно ли создать доверительный интервал для медианы? Да, это возможно, но методы в данном случае более сложные, чем для среднего значения. Обычно применяются методы bootstrap (многократное повторное выборочное оценивание) или подходы, основанные на порядковых статистиках.
- Что делать, если данные имеют ненормальное распределение? Для больших выборок (n>30) можно использовать центральную предельную теорему. В случае малых выборок целесообразно применять непараметрические методы или проводить преобразования данных.
- Как интерпретировать перекрывающиеся доверительные интервалы? Перекрытие интервалов не всегда указывает на отсутствие статистически значимой разницы. Для получения точного вывода требуется использование специальных тестов (например, t-теста для средних значений).
- Почему 95% доверительный интервал стал общепринятым стандартом? Это является компромиссом между точностью (узостью интервала) и уровнем уверенности. Интервалы на уровне 99% слишком широки, в то время как 90% недостаточно надежны для большинства практических задач.
Заключение и практические рекомендации
Доверительные интервалы представляют собой мощный инструмент для статистического анализа, предоставляя более глубокую информацию, чем простые точечные оценки или тесты на значимость. Рекомендуется всегда указывать доверительные интервалы наряду с точечными оценками в ваших исследованиях. Для корректного применения этого метода следует: 1) проверять предпосылки (нормальность распределения, случайность выборки), 2) заранее определять уровень доверия перед началом исследования, 3) обращать внимание на практическую значимость, а не только на статистическую, 4) применять робастные методы (например, bootstrap или непараметрические интервалы) для небольших или аномально распределенных выборок. Освоив данный подход, вы сможете делать более обоснованные выводы на основе данных и избегать распространенных ошибок в статистике. Для более глубокого понимания рекомендую практиковаться с реальными наборами данных и использовать специализированное программное обеспечение, такое как R или Python.
Исторический контекст и развитие концепции доверительных интервалов
Концепция доверительных интервалов (ДИ) имеет свои корни в развитии статистики и теории вероятностей, которые начали активно развиваться в XVIII-XIX веках. Одним из первых, кто начал систематически использовать идеи, связанные с оценкой параметров, был английский математик Томас Байес. Его работы, в частности, привели к формулированию байесовского подхода, который стал основой для многих современных методов статистического анализа.
Однако именно в начале XX века концепция доверительных интервалов получила более четкое определение и применение. В 1930-х годах статистик Уильям Госсет, работая под псевдонимом «Student», разработал метод, известный как t-распределение. Этот метод позволил исследователям оценивать параметры выборки и строить доверительные интервалы для среднего значения, особенно когда размер выборки был мал.
С тех пор доверительные интервалы стали неотъемлемой частью статистического анализа. В 1937 году статистик Джон Тьюки предложил использовать доверительные интервалы для оценки разности средних значений, что открыло новые горизонты для применения этой концепции в различных областях, включая медицину, социологию и экономику.
В 1950-х и 1960-х годах статистическая теория продолжала развиваться, и появились новые методы, позволяющие строить доверительные интервалы для различных параметров и распределений. В это время также началось активное использование компьютерных технологий, что значительно упростило расчеты и сделало методы статистического анализа более доступными.
Сегодня доверительные интервалы используются в самых разных областях науки и практики. Они помогают исследователям и аналитикам делать выводы о популяциях на основе выборок, а также оценивать степень неопределенности в своих результатах. Развитие статистики и вычислительных технологий продолжает влиять на методы построения доверительных интервалов, что делает их еще более точными и полезными инструментами в современном мире.
Вопрос-ответ
В чем смысл доверительного интервала?
Доверительный интервал — это определённый диапазон, который служит для оценки неизвестного параметра с высокой степенью надёжности. Доверительные интервалы используются в аналитике, чтобы определять достоверность результатов расчётов и принимать обоснованные бизнес-решения.
Что такое 95% доверительный интервал?
Как правило, уровень доверия должен быть 95% или 99%. Это значит, что исследователи на 95% (или 99%) уверены, что полученный эффект находится в истинном диапазоне. Например, при определении среднего возраста вместо 15 лет исследователи используют интервал «от 14 до 16 лет».
Как выразить доверительный интервал словами?
Правильная интерпретация 95% доверительного интервала [L, U] заключается в следующем: «мы на 95% уверены, что [параметр популяции] находится между [L] и [U]».
Советы
СОВЕТ №1
Изучите основные понятия статистики, такие как среднее, стандартное отклонение и выборка. Понимание этих терминов поможет вам лучше grasp концепцию доверительного интервала и его применение в анализе данных.
СОВЕТ №2
Используйте визуализацию данных, чтобы лучше понять, как работает доверительный интервал. Графики и диаграммы могут наглядно показать, как изменяется интервал в зависимости от размера выборки и уровня доверия.
СОВЕТ №3
Практикуйтесь на реальных данных. Попробуйте рассчитать доверительный интервал для различных наборов данных, чтобы увидеть, как он меняется в зависимости от условий. Это поможет закрепить теоретические знания на практике.
СОВЕТ №4
Не забывайте о контексте. Доверительный интервал не дает точного ответа, а лишь показывает диапазон, в котором, с определенной вероятностью, может находиться истинное значение. Учитывайте это при интерпретации результатов.